PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசார்புகளின் சேர்ப்பைக் கீழ்க்கண்ட நடைமுறை உதாரணத்துடன் பார்க்கலாம்.
நீங்கள் ஒரு மளிகைக் கடையில் ஒரு வகை பழங்களை வாங்கப் போகிறீர்கள் என்று வைத்துக்கொள்வோம்.
பழங்களுக்கான விலைப்பட்டியல் ஒவ்வொரு பழத்தின் எடையையும் அடிப்படையாகக் கொண்டது.
சார்புகளின் சேர்ப்பு இங்குதான் நடைபெறுகிறது.
ஒவ்வொரு பழத்தையும் எடையிடும் இயந்திரத்தில் ஏற்றுகிறீர்கள்.
நீங்கள் வாங்கும் ஒவ்வொரு பழத்தின் எடையின் அடிப்படையில் அதன் விலையைக் காண்பிக்கும் வகையில் இந்த அமைப்பு திட்டமிடப்பட்டுள்ளது.
\(A\) என்பது பழங்களின் கணம் என்க.
\(B \subset \mathbb{R}\) என்பது எடை என்க.
\(C \subset \mathbb{R}\) என்பது விலை என்க.
இந்தச் செயல்பாடு கீழ்க்கண்ட அம்புகுறி படம் மூலம் நடைபெறுகிறது.
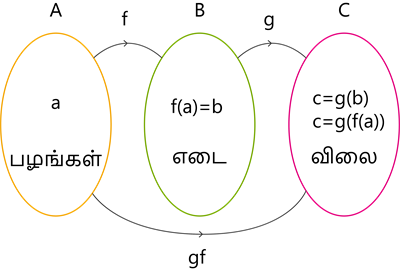
இந்தச் செயல்பாடு \(f: A \rightarrow B\) மற்றும் \(g: B \rightarrow C\) என்ற இரண்டு சார்பைத் தருகிறது. \(b = f(a)\) என்பது எடை \(a\) மற்றும் \(c = g(b)\) என்பது \(b\) எடை உள்ள பொருட்களின் விலை, இங்கு \(a \in A\), \(b \in B\) and \(c \in C\).
இந்தச் செயல்பாட்டை, கணித முறையில் கீழ்க்கண்டவாறு எழுதலாம்.
\(c = g(b) = g\left(f(a)\right)\)
எனவே, மேற்கூறிய இரண்டு செயல்பாடுகளையும் இணைப்பதன் மூலம், ஒவ்வொரு பழமும் இறுதியில் ஒரு குறிப்பிட்ட விலையுடன் மதிப்பிடப்படுகிறது.
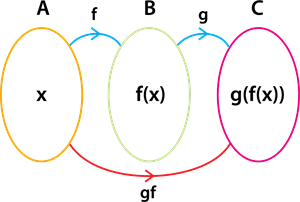
இந்த விளக்கத்தின் அடிப்படையில், இரண்டு செயல்பாடுகளின் கலவையை பின்வருமாறு வரையறுப்போம்.
\(f: A \rightarrow B\) மற்றும் \(g: B \rightarrow C\) என்பன இரண்டு சார்புகள் என்க. எனவே, \(f\) மற்றும் \(g\) சேர்ப்பு \(g \circ f\) ஆனது \(g \circ f(x) = g\left(f(x)\right)\) \(\forall x \in A\) என வரையறுக்கப்படுகிறது.
Register for free to see more content