அடிப்படை எண்ணியல் தேற்றம்

PDF chapter test TRY NOW

தேற்றம்:

$1$ ஐத் தவிர்த்து, அனைத்து மிகை முழுக்களையும் ஒரு பகா எண்ணாக அல்லது பகா எண்களின் பெருக்கற்பலனாகக் காரணிப்படுத்த முடியும். மேலும் இந்த காரணிப்படுத்தலானது பகா எண்கள் எழுதப்படும் வரிசையைத் தவிர்த்து ஒரே முறையில் அமையும்.

விளக்கம்:

$N$ என்பது ஏதேனும் ஒரு பகு எண் என்க.

$N$ ஐ பகா காரணிகளாக கீழ்கண்டவாறு பிரிக்கலாம்.

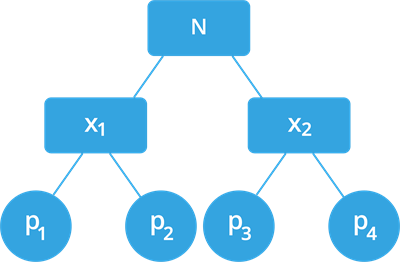
$N = x_1 \times x_2$ .

இங்கு,

$x_1$ மற்றும்

$x_2$ என்பன மேலும் இரு பகு காரணிகள்.

எனவே, இவற்றை மீண்டும் காரணிப்படுத்த வேண்டும்.

$x_1 = p_1 \times p_2$ .

$x_2 = p_3 \times p_4$ .

எனவே,

$N = p_1 \times p_2 \times p_3 \times p_4$ இங்கு,

$p_1$ ,

$p_2$ ,

$p_3$ and

$p_4$ என்பன பகா எண்கள்.

சில நேரங்களில் சில பகா எண்கள் மீண்டும் மீண்டும் காரணிகளாக வரலாம். அப்படி வரும் நேரங்களில் பகா எண்களை அடுக்குகளாக எழுத வேண்டும்.

$N$ என்ற மிகை முழு

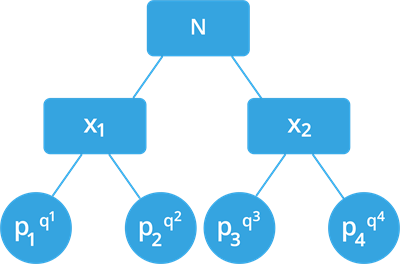
$N = {p_{1}}^{q_{1}} \times {p_{2}}^{q_{2}} \times {p_{3}}^{q_{3}} \times ... \times {p_{n}}^{q_{n}}$ என்றவாறு காரணிப்படுத்தப்படுகிறது. இங்கு,

$p_{1}, p_{2}, p_{3}, ... p_{n}$ என்பது பகா எண்கள்.

$q_{1}, q_{2}, q_{3}, ... q_{n}$ என்பது இயல் எண்கள்.

Example:

$26950$ என்ற எண்களை எடுத்துக்கொள்வோம்.

கீழ்கண்டவாறு

$26950$ என்ற எண்ணைக் காரணிப்படுத்தலாம்.

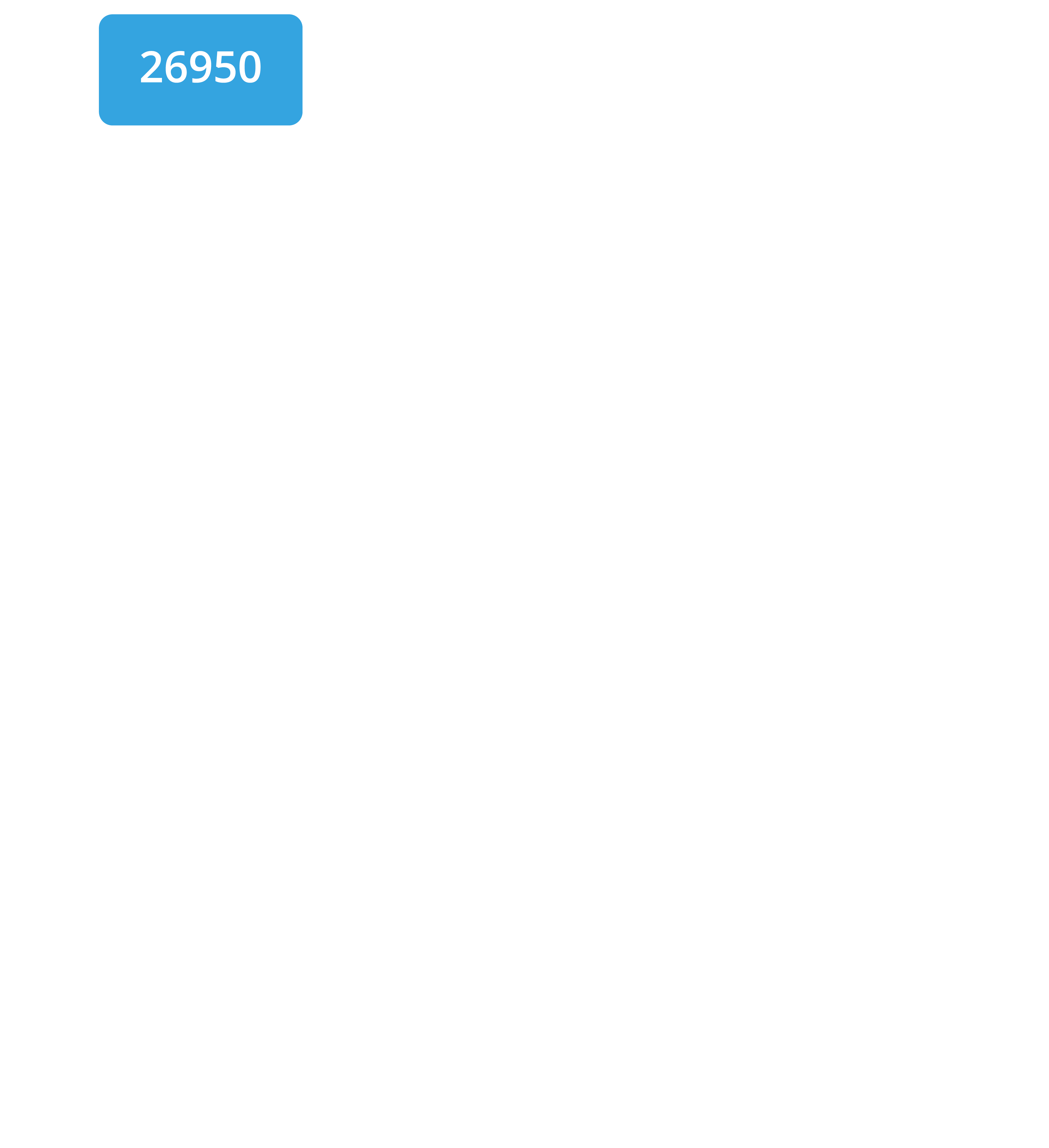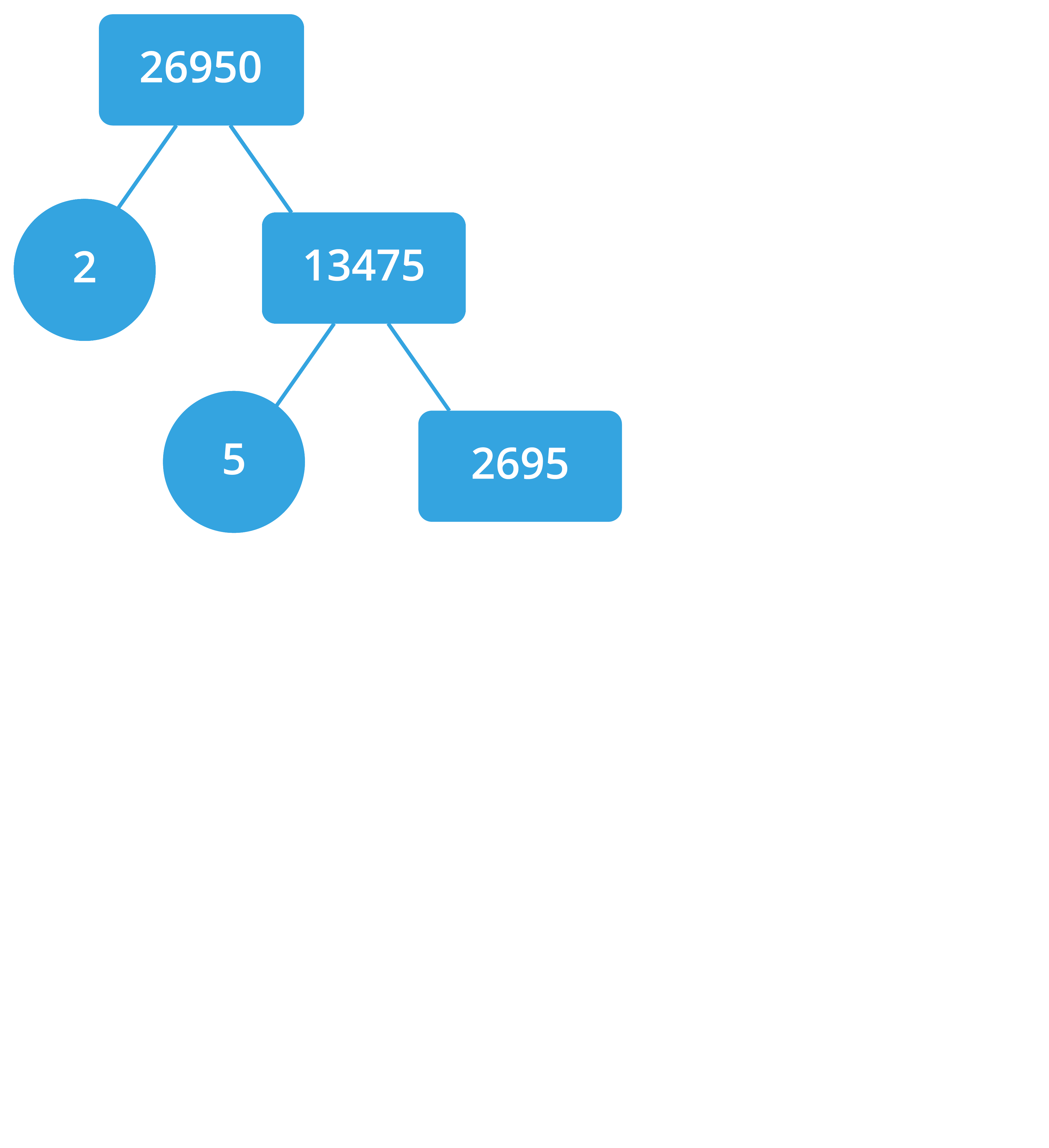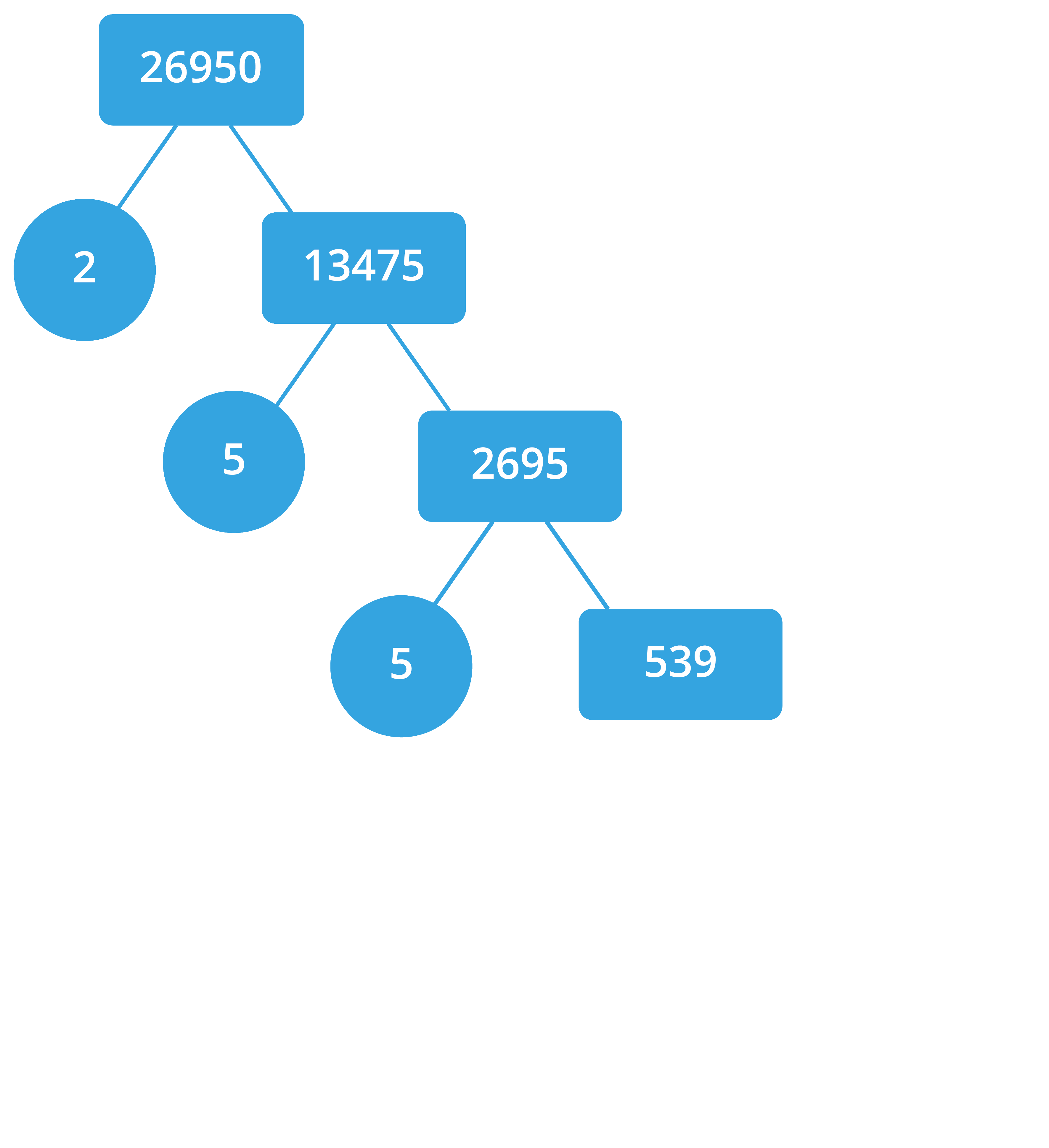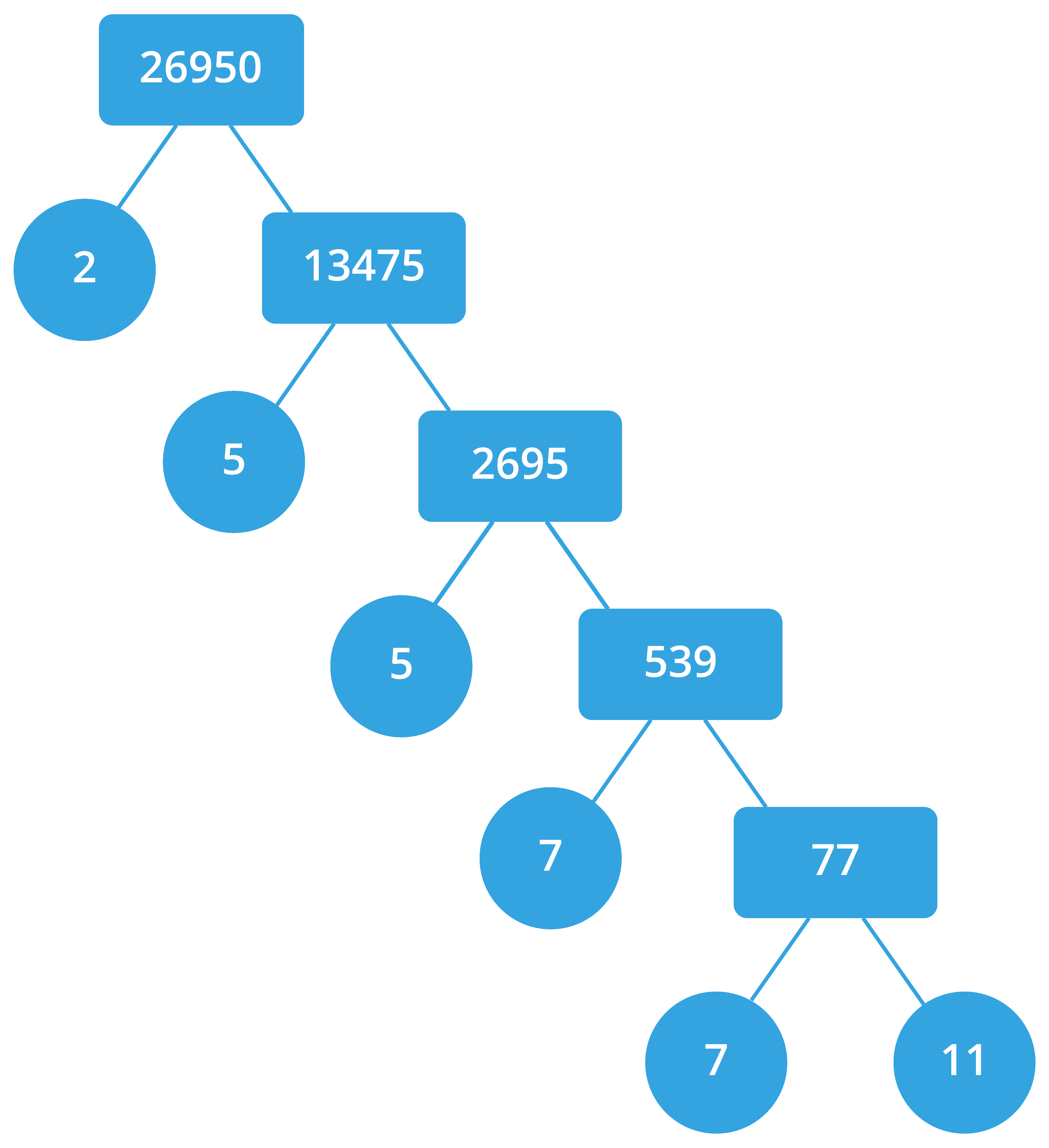
எனவே,

$26950$

$=$

$2 \times 5 \times 5 \times 7 \times 7 \times 11$ .

அதாவது,

$26950 = 2 \times 5^2 \times 7^2 \times 11$ .

இங்கு,

$26950$ என்பது பகா காரணிகளாகப் பிரிக்கப்பட்டுள்ளது.

பகா எண்களின் வரிசையை மாற்றினாலும்

$26950$ என்ற எண் கிடைக்கும்.

எனவே,

$26950$ ஐ

$26950 = 2 \times 7^2 \times 5^2 \times 11$ அல்லது

$26950 = 11 \times 7^2 \times 5^2 \times 2$ என எழுதலாம்.

பகா காரணிகள் வரிசையைப் பொறுத்தது அல்ல.

Important!

மீ.பொ.வ

$=$ எண்களில் உள்ள பொதுவான காரணிகளின் சிறிய அடுக்குகளின் பெருக்கற்பலன்.

மீ.சி.ம

$=$ எண்களில் உள்ள பொதுவான காரணிகளின் பெரிய அடுக்குகளின் பெருக்கற்பலன்.

Previous topic

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

1. அடிப்படை எண்ணியல் தேற்றம்

Theory: