PDF chapter test TRY NOW
கொடுக்கப்பட்ட இரண்டு அல்லது அதற்கு மேற்பட்ட எண்களின் மீப்பெரு பொதுக் காரணி(மீ. பொ. வ) அவற்றின் பொது காரணிகளின் மிகப்பெரிய எண்ணிக்கையாகும். இது மீப்பெரு பொது வகுத்தி (மீ. பொ. வ)என்றும் அழைக்கப்படுகிறது.
இரண்டு அல்லது அதற்கு மேற்பட்ட எண்களின் மீ.பொ.வ ஐக் கண்டறிய, பின்வரும் முறைகளில் ஏதேனும் ஒன்றைப் பயன்படுத்தலாம்.
1. பொது காரணி முறை
2. வகுத்தல் முறை
பொது காரணி முறை மூலம் மீ.பொ.வ:
18 மற்றும் 24 மீ.பொ.வ வை கீழ்கண்டவாறு காணலாம்.
முதலில், கொடுக்கப்பட்ட எண்களின் அனைத்து காரணிகளையும் கண்டறிய வேண்டும்.
| 1 \times 18 =18 | 2 \times 9 = 18 | 3 \times 6 = 18 | 18 \times 1 =18 | 9 \times 2 = 18 | 6 \times 3 = 18 |
18 = ன் காரணிகள் 1, 2, 3, 6, 9, 18.
| 1 \times 24 = 24 | 2 \times12 = 24 | 3 \times 8 = 24 | 4 \times 6 = 24 | 6 \times 4 = 24 | 8 \times 3 = 24 | 12 \times 2 = 24 | 24 \times 1 = 24 |
காரணிகள் 24 = 1, 2, 3, 4, 6, 8, 12, 24.
18 மற்றும் 24 இன் பொது காரணிகள் 1, 2, 3 மற்றும் 6.
மேலே உள்ள பொது காரணிகளில் மிக உயர்ந்த பொது காரணி 6.
எனவே, 18 மற்றும் 24 இன் மீ.பொ.வ 6 ஆகும்.
வகுத்தல் முறையின் மீ.பொ.கா காணுதல்:
1.27 மற்றும் 45 மீ.பொ.கா வைக் கீழ்கண்டவாறு காணலாம்.
முதலில், 27 முக்கிய காரணிகளைக் கண்டறிய வேண்டும்.
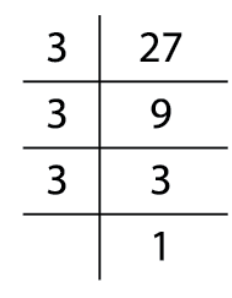
27=3\times 3\times 3
இப்போது, 45 முக்கிய காரணிகளைக் கண்டறியவும்.
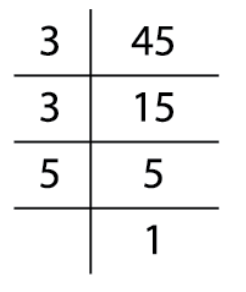
45 = 3 \times 3 \times 5
27 மற்றும் 45 இன் பகா காரணியாக்கம்:
27 = 3 \times 3 \times 3
45 = 3 \times 3 \times 5
27 மற்றும் 45 பொது காரணிகளை எடுத்துக் கொள்ளுங்கள்.
3 \times 3 = 9
எனவே, 27 மற்றும் 45 இன் மீ.பொ.வ 9 ஆகும்.
பகா காரணியாக்க முறை மூலம் மீ.பொ.வ ஐக் கண்டுபிடிப்போம்.
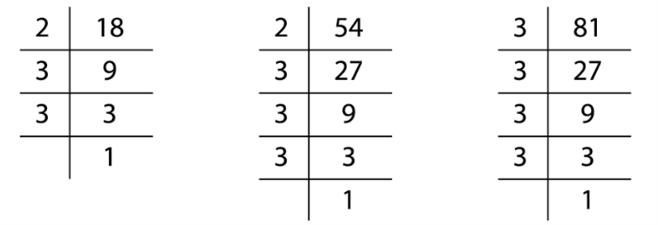
18 = 2 \times 3 \times 3
54 = 2 \times 3 \times 3 \times 3
81 = 3 \times 3 \times 3 \times 3
3 \times 3 = 9
எனவே, 18, 54 மற்றும் 81 இன் மீ.பொ.வ 9 ஆகும்.
Register for free to see more content