PDF chapter test TRY NOW
கணினிகள் எவ்வாறு விரைவாக கணக்கீடுகளைச் செய்கின்றன என்று நீங்கள் எப்போதாவது யோசித்திருக்கிறீர்களா?
அன்றாட வாழ்க்கையில் கணினிகள் முக்கிய பங்கு வகிக்கின்றன. இது நம் வாழ்வில் மிகவும் முக்கியமானதாகிவிட்டது, ஏனெனில் இது மிகச் சிறிய கடைகளில் இருந்து பெரிய தொழில்களில் பயன்படுத்தப்படுகிறது. கணினிகளின் பயன்பாடு அதன் வேகம், துல்லியம் மற்றும் ஒரு நொடியில் பில்லியன் கணக்கான வழிமுறைகளை செயலாக்கும் திறன் ஆகியவற்றின் காரணமாக பெருமளவில் வளர்ந்துள்ளது. கணினி வழங்கிய கணக்கீட்டு முடிவு சரியாக இருக்கும், மேலும் சரிபார்க்க வேண்டிய அவசியமில்லை. கணினிகள் அனைத்து கணக்கீடுகளையும் மரவுரு வரைபடங்களாக மாற்றுவதன் மூலம் செய்கின்றன.
இந்த பகுதியில், இயற்கணித கோவை/எண் கோவையை மரவுரு வரைபடமாகவும், மரவுரு வரைபடத்தை எண் கோவை/இயற்கணித கோவை மாற்றுவது எப்படி என்பதைக் கற்றுக்கொள்வோம்.
மரவுரு வரைபடம் என்றால் என்ன?
கீழ்கண்ட எடுத்துக்காட்டு மூலம் மரவுரு வரைபடம் பற்றி விரிவாக காணலாம்.
Example:
\([(6 + 2) \div 4]\) \(\times\) \(3\) என்ற கோவையை மரவுரு வரைபடமாக மாற்றுக.
தீர்வு:
1. \(a_1 = b_1 \div y_1\), \(a_2 = 3\), \(b_1 = x_1 + x_2\), \(x_1 = 6\), \(x_2 = 2\), \(y_1 = 4\) என எடுத்துக்கொள்வோம்.
2. முதல் கோவைக்கு மரவுரு வரைபடம் வரைக.
3. \(a_1\) க்கு மரவுரு வரைபடம் வரைக.
இங்கு, \(a_1 = b_1 \div y_1\), \(b_1 = 6 + 2\) மற்றும் \(y_1 = 4\).
4. \(b_1 = x_1 + x_2\) என எடுத்துக் கொள்வோம்.
இங்கு, \(x_1 = 6\), \(x_2 = 2\)
5. கொடுக்கப்பட்ட மதிப்புகளை பிரதியிட்டு இவை அனைத்தையும் ஒன்றாக இணைத்தால் நமக்குப் பின்வரும் மரவுரு வரைபடம் கிடைக்கின்றது.
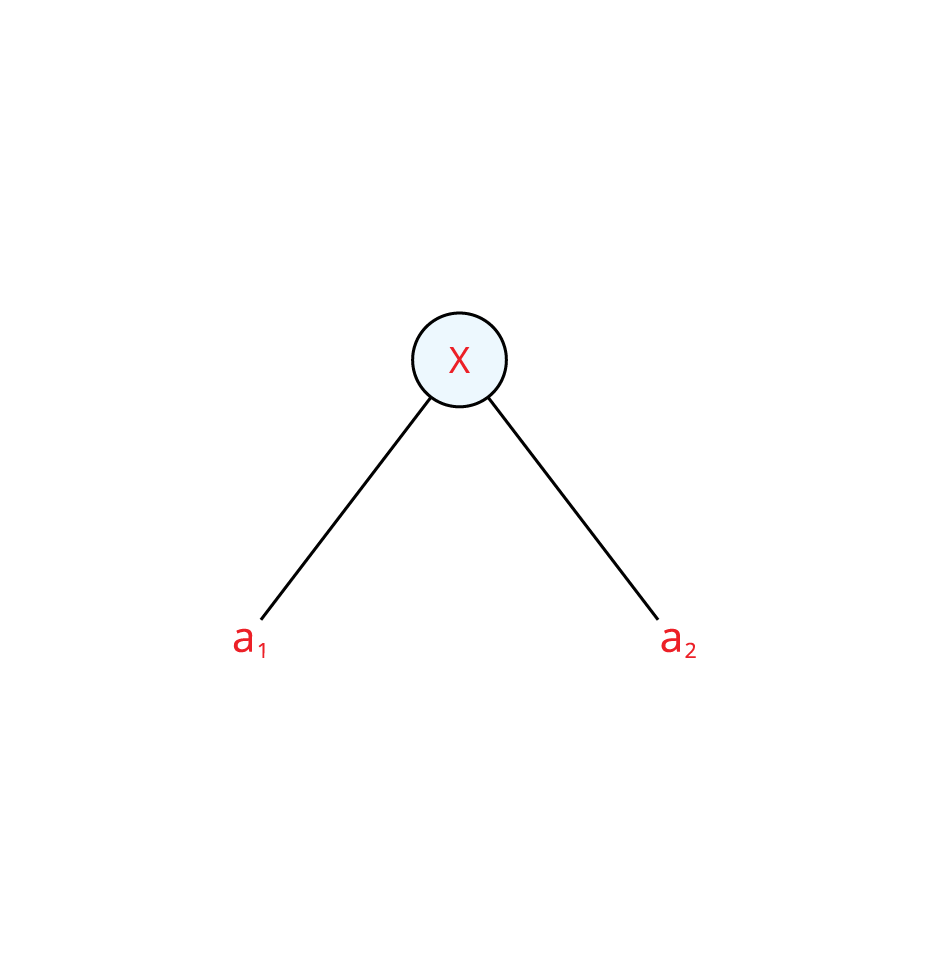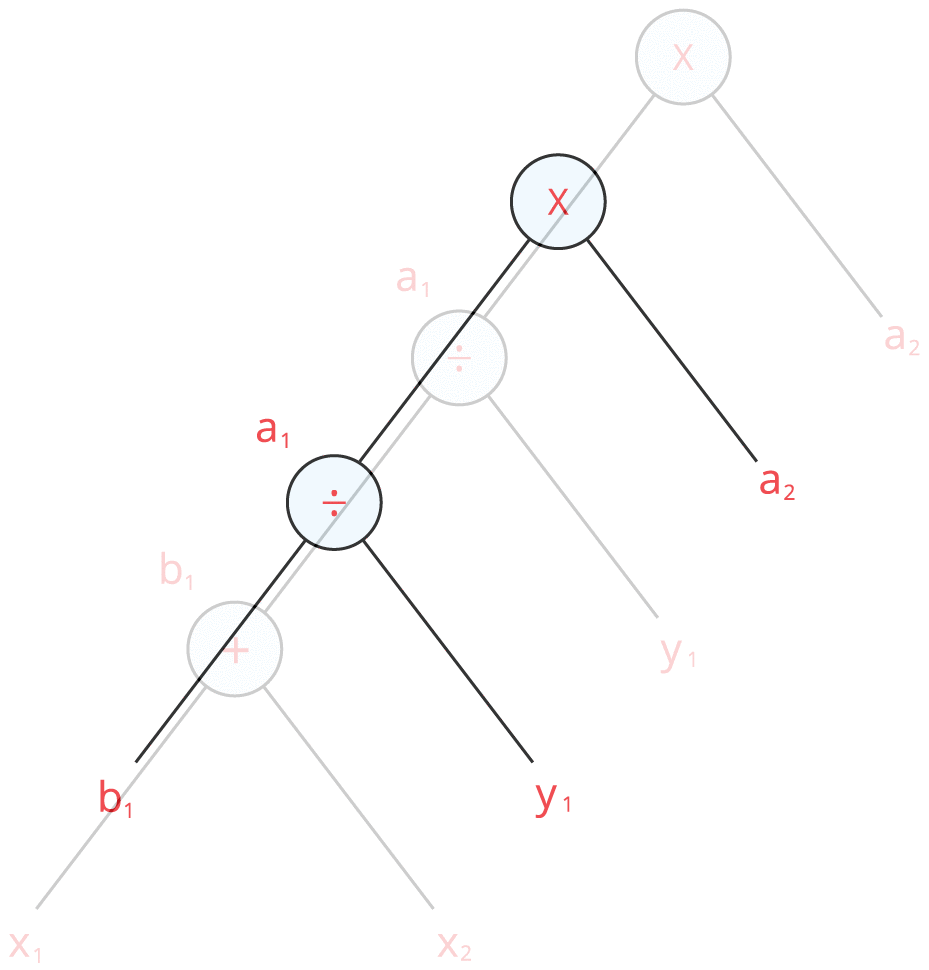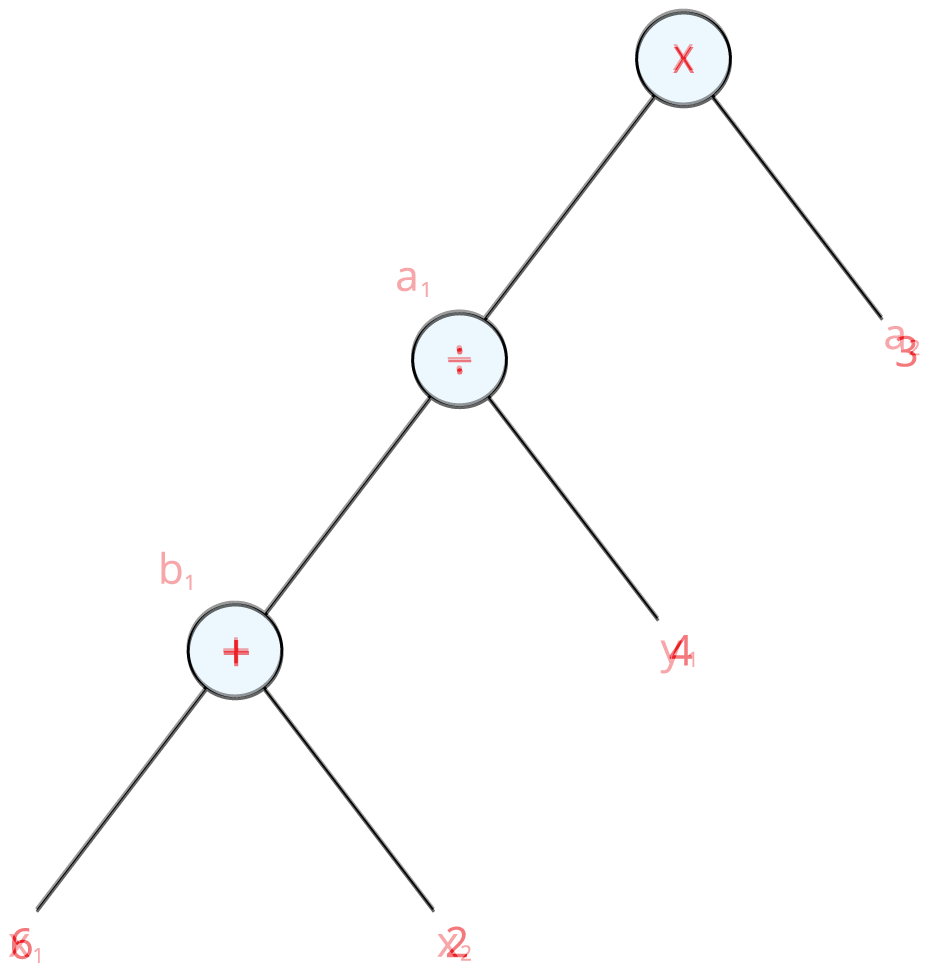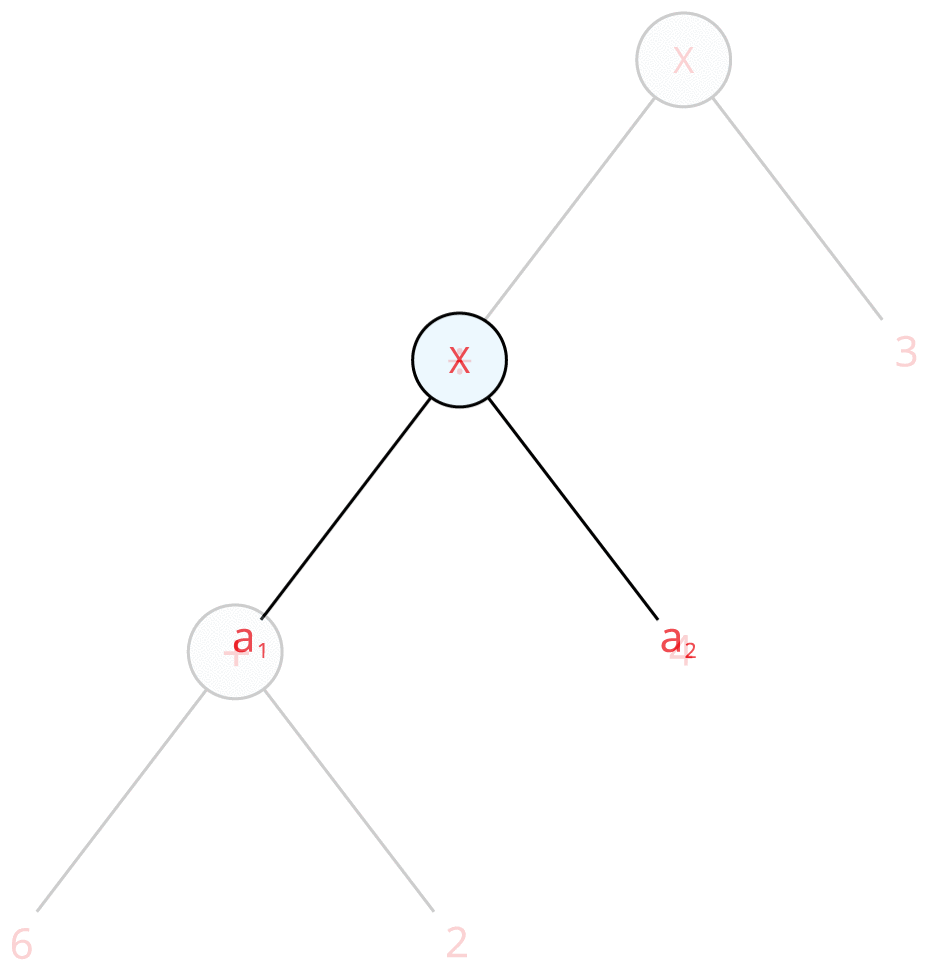
மேலே உள்ள வரைபடத்திலிருந்து, ஒவ்வொரு முனைக்கும் ஒன்று அல்லது இரண்டு கிளைகள் இருப்பதையும், ஒவ்வொரு முனையிலும் ஒரு செயல்பாடு இருப்பதையும் காணலாம். நாம் தலைகீழாகப் பார்க்கும்போது மரத்தைப் போலத் தெரிவதால் இந்த வரைபடம் மரவுரு வரைபடம் என்று அழைக்கப்படுகிறது. இங்கே, வேர் மேல் மற்றும் இலைகள் கீழே உள்ளன.
இயற்கணித கோவையை மரவுரு வரைபடமாக மாற்றவது பற்றி எடுத்துக்காட்டு மூலம் அறியலாம்.
\(5a + 2b\) என்ற இயற்கணித கோவையை மரவுரு வரைபடமாக வரைக.
தீர்வு:
\(5a + 2b\) என்ற இயற்கணித கோவையை கீழ்கண்டவாறு மரவுரு வரைபடமாக மாற்றலாம்.
Register for free to see more content