PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஇயற்கணிதக் கோவையின் படி என்றால் என்ன ?
ஒரு கோவையின் படியை அறிவதற்கு, முதலில் ஒரு மாறியின் படியினை அடுக்கு எண்களுடன்
தொடர்பு படுத்த வேண்டும்.
மாறியின் அடுக்குகள்:
சதுரத்தின் பக்க அளவு x.
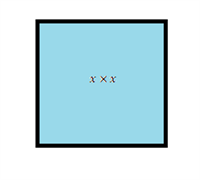
சதுரத்தின் பகுதி = x \times x = x^2 \ சதுர.
x^2 என்னும் கோவையில் ஒரு உறுப்பு உள்ளதால் அதனை ஓர் உறுப்புக் கோவை என்று அழைக்கிறோம்.
செவ்வகத்துடைய நீளம் l மற்றும் அகலம் b.
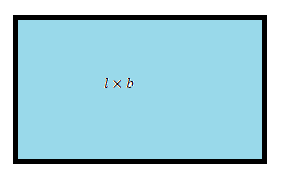
செவ்வகத்தின் பகுதி = l \times b sq. \ units
l^1b^1. இப்பொழுது அடுக்குகளை நாம் கூட்ட வேண்டும். அவை 1 + 1 =2.
lb இக் கோவையில் உள்ள அடுக்கு எண் 2 ஆகும்.
Example:
1. 3y^2 + y +2 என்ற எண்ணிற்கு இயற்கணிதக் கோவையின் படியைக் கண்டுப்பிடிக்கவும்.
விடை:
3y^2 இக் கோவையில், y இன் அடுக்கு 2. எனவே 3y^2 இதன் படி 2 ஆகும், எனவே y இதன் படி 1 ஆகும்.
3y^2 இதனுடைய பெரிய அடுக்கு 2 ஆகும்.
2, இதுவே இக்கொவையின் படி ஆகும்.
2. 2x^2 +3xy^4 +y+6 என்ற எண்ணிற்கு இயற்கணிதக் கோவையின் படியைக் கண்டுப்பிடிக்கவும்.
விடை:
கொடுக்கப்பட்டுள்ள கோவையில் உள்ள மாறிகள் 2x^2, 3xy^4, y மற்றும் 6.
2x^2 உடைய அடுக்கு 2 ஆகும்.
3xy^4 இதனுடைய அடுக்கு 1 + 4 = 5 ஆகும்.
y உடைய அடுக்கு 1 ஆகும்.
3xy^4 இதனுடைய பெரிய அடுக்கு 5 ஆகும்.
5 இதுவே இக் கோவையின் படி ஆகும்.
Register for free to see more content