PDF chapter test TRY NOW
தேற்றத்தின் கூற்று:
ஒரு செங்கோண முக்கோணத்தில் கர்ணத்தின் மீதமைந்த சதுரத்தின் பரப்பளவானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின் பரப்பளவுகளின் கூடுதலுக்குச் சமமாகும்.
செங்கோண முக்கோணம் ABC இல், AC^2=AB^2+BC^2.
கொடுக்கப்பட்டது:
ABC என்பது ஒரு செங்கோண முக்கோணம்.
அதாவது, \angle ABC = 90^{\circ}.
நிரூபிக்க வேண்டியது:
AC^2=AB^2+BC^2
நிரூபணம்:
B லிருந்து AC க்கு BD \perp AC என்றவாறு BD என்ற நேர்க்கோடு வரைக.
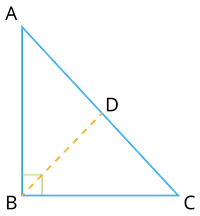
ABC மற்றும் BDC என்ற முக்கோணங்களை எடுத்துக்கொள்வோம்.
\angle C என்பது இரண்டு முக்கோணங்களுக்கும் பொதுவான கோணம் ஆகும்.
இங்கு, BD \perp AC.
எனவே, \angle BDC = 90^{\circ}.
மேலும், \angle ABC = 90^{\circ}.
கோ-கோ வடிவொத்தப் பண்பின்படி,(ஒரு முக்கோணத்தின் இரண்டு கோணங்கள், மற்றொரு
முக்கோணத்தின் இரண்டு கோணங்களுக்குச் சமம் எனில், அவ்விரு
முக்கோணங்களும் வடிவொத்தவை ஆகும்.) ABD மற்றும் BDC ஆகிய முக்கோணங்கள் வடிவொத்தவை.
எனவே, முக்கோணங்களின் பக்கங்களின் விகிதம் சமம் ஆகும்.
அதாவது, \frac{BC}{CD} = \frac{AC}{BC}.
இதன் மூலம், BC^{2} = AC \times CD ……(1)
தற்பொழுது, ABC மற்றும் ABD என்ற முக்கோணங்களை எடுத்துக்கொள்வோம.
மீண்டும் கோ-கோ பண்பின்படி, \frac{AB}{AD} = \frac{AC}{AB}.
இதன் மூலம், AB^{2} = AC \times AD ……(2)
(1) மற்றும் (2) வது சமன்பாட்டை கூட்ட,
BC^2 + AB^2 = (AC \times CD) + (AC \times AD)
= AC (CD +AD)
= AC \cdot AC
= AC^2.
எனவே, AC^2 = AB^2 + BC^2.
பிதாகரஸ் தேற்றம் நீருபிக்கப்பட்டது.
Example:
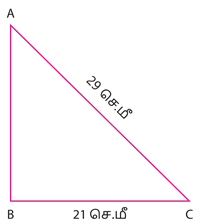
ஒரு செங்கோண முக்கோணத்தில் கர்ணம் 29 செ.மீ ஒரு பக்கம் 21 செ.மீ எனில் மற்றொரு பக்கத்தின் நீளம் காண்க:
தீர்வு:
ABC என்பது ஒரு செங்கோண முக்கோணத்தை படத்தில் காட்டியவாறு எடுத்துக்கொள்வோம்.
இங்கு, AC என்பது கர்ணம் ஆகும்.
பிதாகரஸ் தேற்றத்தின்படி, AC^2 = AB^2 + BC^2.
எனவே, AB^2 = AC^2 - BC^2.
\Rightarrow AB^2 = 29^2 -21^2
= 841 - 441
= 400
AB = \sqrt{400}.
AB = 20
எனவே, மற்றொரு பக்கத்தின் நீளம் 20 செ.மீ.
