PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoகாட்சி விளக்கம்:
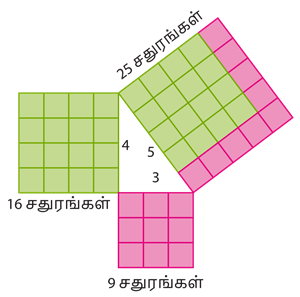
இந்த காட்சி விளக்கம் மூலம் பிதாகரஸ் தேற்றத்தினை எளிமையாக அறியலாம்.
படத்தில் ஒரு செங்கோண முக்கோணம் 6 அலகுகள்;, 8 அலகுகள் மற்றும் 10 அலகுகள் பக்கங்களாக கொண்டு அமைவதைக் காணலாம்.
இப்படத்தில் 6 அலகுகள் மற்றும் 8 அலகுகள் ஆகிய அளவுகளைக்
கொண்ட பக்கங்கள் செங்கோணத்தைத் தாங்கும் பக்கங்கள் ஆகும்.
10 அலகுகள் அலகுகள் கொண்ட பக்கமானது கர்ணம் என அழைக்கப்படுகிறது.
கர்ணம் என்பது செங்கோண முக்கோணத்தின் மிகவும் நீளமான
பக்கம் ஆகும்.
6 அலகுகள் பக்கமாக கொண்ட சதுரத்தின் பரப்பளவு= 6 \times 6 = 36 சதுர அலகுகள்.
8 அலகுகள் பக்கமாக கொண்ட சதுரத்தின் பரப்பளவு= 8 \times 8 = 64 சதுர அலகுகள்.
10 அலகுகள் பக்கமாக கொண்ட சதுரத்தின் பரப்பளவு'= 10 \times 10 = 100 சதுர அலகுகள்.
இங்கு, 100 சதுர அலகுகள் = 36 சதுர அலகுகள் + 64 சதுர அலகுகள்.
அதாவது, 10^2 = 6^2 + 8^2.
மேற்கண்ட சமன்பாடு ஒரு செங்கோண முக்கோணத்தில் கர்ணத்தின் மீதமைந்த சதுரத்தின்
பரப்பளவானது, மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின்
பரப்பளவுகளின் கூடுதலுக்குச் சமமாக இருப்பதை விளக்குகிறது.
பிதாகரஸ் தேற்றத்தின் மறுதலை:
ஒரு முக்கோணத்தின் நீளமான பக்கத்தின் மீதமைந்த சதுரத்தின் பரப்பளவானது,
மற்ற இரண்டு பக்கங்களின் மீதமைந்த சதுரங்களின் பரப்பளவுகளின் கூடுதலுக்குச்
சமம் எனில், அந்த முக்கோணம் செங்கோண முக்கோணம் ஆகும்.
விளக்கம்:
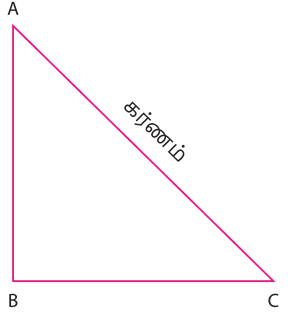
முக்கோணம் ABC யில், AC^2 = AB^2 + BC^2 எனில் முக்கோணம் ABC ஒரு செங்கோண முக்கோணம் ஆகும். இங்கு,\angle B = 90^{\circ}.
Example:
மேலேக் கொடுக்கப்பட்ட காட்சி விளக்கத்தில் 6 அலகுகள், 8 அலகுகள் மற்றும் 10 அலகுகள் கொண்ட முக்கோணத்தின் பக்கத்தில்,
முக்கோணத்தின் கர்ணம் 10 அலகுகள், மற்றும் பக்கங்கள் 6 அலகுகள் மற்றும் 8 அலகுகள்.
கரணத்தின் வர்க்கம் = 10^2 = 100
பக்கங்களின் வர்க்கங்களின் கூடுதல்= 6^2 + 8^2 = 36 + 64 = 100
இங்கு, கர்ணத்தின் வர்க்கமானது மற்ற இரு பக்கங்களின் வர்க்கங்களின் கூடுதலுக்கு சமம்.
எனவே, பிதாகரஸ் தேற்றத்தின் மறுதலைப் படி, கொடுக்கப்பட்ட முக்கோணம் செங்கோண முக்கோண ஆகும்.
(i) x, y மற்றும் z என்ற முழுக்கள் பிதாகரஸ் தேற்றத்தை பூர்த்தி செய்தால் இதனை பிதாகோரியன் மூன்றன் தொகுதி என அழைக்கலாம்.
Example:
(12, 13, 15) என்பது பிதாகோரியன் மூன்றன் தொகுதி ஆகும்.
(ii) l என்பது ஒரு மிகை முழு மற்றும் (x, y, z) என்பது பிதாகோரியன் மூன்றன் தொகுதி எனில் (lx, ly, kz) என்பதும் பிதாகோரியன் மூன்றன் தொகுதி ஆகும்.
Register for free to see more content