வர்க்கமூலச் சுருள் அமைக்கும் செய்முறை

PDF chapter test TRY NOW

கணிப்பங்களைக் கண்டறிவதற்கு முன்பே இந்த செயல்முறை கண்டறியப்பட்டது. விகிதமுறா எண்ணின் தோராயமான மதிப்பைக் கண்டுபிடிப்பது கடினமானது.

பழங்கால கணிதவியலாளர்கள் பக்க நீளம்

$1$ அலகு கொண்ட சதுரம்,

$\sqrt{2}$ மூலைவிட்ட நீளம், சமன்பாடு பட அலகுகளைக் கொடுக்கும் என்ற உண்மையைப் பயன்படுத்தினர். மூலைவிட்ட நீளத்தை பக்க நீளமாக எடுத்துக்கொண்டு, மற்றொரு பக்க நீளத்தை

$1$ அலகு என்று எடுத்துக்கொண்டால், அந்த முக்கோணத்தின் மூலைவிட்ட பக்கம்

$\sqrt{3}$ அலகு இருக்கும். அலகு பக்க நீளத்தை மீண்டும் மீண்டும் நீட்டித்தால், எந்த எண்ணின் வர்க்க மூலமும் கிடைக்கும்.

எனவே, நமக்கு பின்வரும் உண்மைகள் கிடைக்கப்பெறுகிறது:

எந்தவொரு நேர்மறை முழு எண் -

$n$ ற்கும்

$\sqrt{n}$ -ஐக் கண்டறியலாம்'

$\sqrt{n - 1}$ ஐக் கண்டறிந்தபின்.

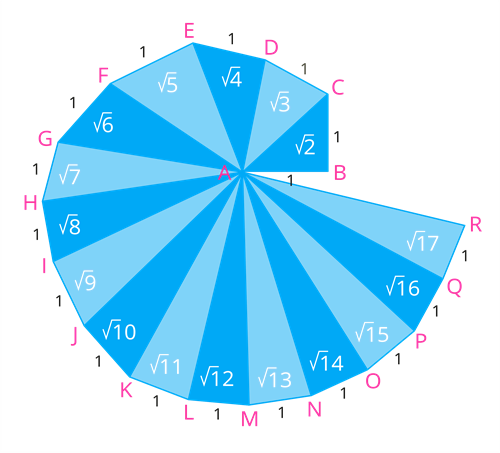
புள்ளி

$A$ ஐக் கண்டறிந்து,

$AB$ நீளம்

$1$ அலகு கொண்ட ஒரு கோடு பகுதியை வரையவும்.

$AB$ க்கு செங்குத்தாக இருக்கும்

$1$ அலகு நீளத்தின்

$BC$ கோடு பகுதியை வரையவும்.

$AC$ யை இணைக்கவும். தற்பொழுது நம்மிடத்தில்

$ABC$ என்கிற செங்கோண முக்கோணம் உள்ளது மற்றும்

$AB = BC = 1$ அலகு. பிதாகரஸ் தேற்றத்தின் படி

$AC$ இன் மதிப்பு

$\sqrt{2}$ ஆகும்.

$AC$ க்கு செங்குத்தாக இருக்கும்

$1$ அலகு நீளம் கொண்ட கோடு பிரிவு

$CD$ யை வரையவும்.

$AC$ ,

$AD$ ,

$AE$ , … போன்ற கோட்டுத்துண்டுகளால் ஆன வர்க்கமூல சுருளை உருவாக்க செயல்முறையை மீண்டும் செய்யவும்.

இங்கு AC, AD, AE , … குறிக்கும் நீளங்கள்

$\sqrt{2}$ ,

$\sqrt{3}$ ,

$\sqrt{4}$ ,

$\sqrt{5}$ ,

$\sqrt{6}$ ,

$\sqrt{7}$ ,

$\sqrt{8}$ ,

$\sqrt{9}$ ,

$\sqrt{10}$ ,

$\sqrt{11}$ ,...

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

6. வர்க்கமூலச் சுருள் அமைக்கும் செய்முறை

Theory: