விகிதமுறா எண்களின் சில கோட்பாடுகள்

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

விகிதமுறா எண்கள்

π (pi)

\(=\) \(3.141592653589793...\) மற்றும்

ϕ (தங்க விகிதம்)

\(= 1.618033988749894...\)

கிரேக்க கணிதவியலாளர் ஆர்க்கிமிடிஸ்

π (pi)

இன் தசம விரிவாக்கத்தில் இலக்கங்களைக் கணக்கிட்டவர்.

அவர்

π

யின் மதிப்பை \(3.140845 < \pi < 3.142857\) வரம்பிற்கு இடையில் கண்டுபிடித்தார்.

(\(476\) – \(550\) C.E.) காலத்தில், சிறந்த இந்தியக் கணிதவியலாளரும் வானவியலாளருமான ஆர்யபட்டா, \(pi\)யின் மதிப்பை நான்கு தசம இடங்களுக்குச் சரியாகக் கண்டறிந்தார் \(3.1416\).

அதிவேக கணினிகள் மற்றும் மேம்பட்ட நெறிமுறைகளின் உதவியுடன், \(\pi\)யின் தசமங்கள் \(1.24\) டிரில்லியன் தசம இடங்களுக்கு மேல் கணக்கிடப்பட்டுள்ளது!

\(pi\) இன் பயன்பாடுகள்:

கணிதத்தில், இது புள்ளியியல், எண் கோட்பாடு மற்றும் வடிவியல் போன்ற பல்வேறு துறைகளை உள்ளடக்கியது. முக்கோணவியல் துறையில் சைன், கொசைன், டேன்ஜென்ட்... போன்ற முக்கோணவியல் செயல்பாட்டின் மதிப்பைப் பெற இது பயன்படுகிறது.
தெர்மோடைனமிக்ஸ், மெக்கானிக்ஸ் மற்றும் மின்காந்தவியல் போன்ற அறிவியல் பிரிவின் சூத்திரங்கள். சக்கரம், மோட்டார் தண்டுகள், இயந்திர பாகங்கள், கியர்கள் போன்றவற்றின் வட்ட வேகத்தை அளவிட இது பயன்படுகிறது.
கணினியின் வேகத்தைச் சரிபார்க்க, \(pi\)யின் மதிப்பைக் கண்டறிகிறோம். ஏனெனில் அவர்கள் அதன் துல்லியத்தை சரிபார்க்க அதைப் பயன்படுத்தலாம்.

தங்க விகிதம் ஓர் சிறப்பு எண். ஒரு வரியை இரண்டு பகுதிகளாகப் பிரிக்கும்போது நம்மால் தங்க விகிதத்தைப் பெறலாம்..

\(AB\) என்கிற கோட்டுத்துண்டுகளை எடுத்துக்கொண்டு அதை \(AC\) மற்றும் \(CB\) என இரண்டு சிறிய பிரிவுகளாக பிரிக்கவும். அதாவது \(AC=a\) மற்றும் \(BC=b\).

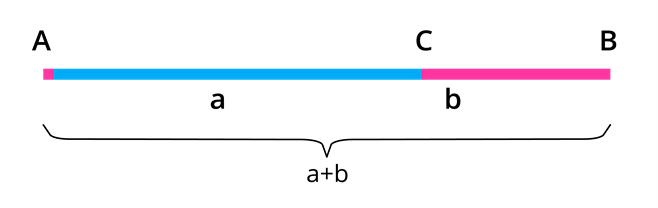
முழு கோட்டுத்துத்துண்டு \(AB = a+b\) விற்கும் \(AC = a\) விற்கும் இடையே உள்ள விகிதமானது கோட்டுத்துத்துண்டு \(AC = a\) விற்கும் \(BC= b\) இடையே உள்ள விகிதமே. இதையே நாம் தங்க விகிதம் எனக் கூறுகிறோம்.

\(a+b : a = a : b\)

அதாவது,