PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமுந்தைய வகுப்புகளில் படித்த பல்லுறுப்பு கோவையினை சற்று நினைவுப்படுத்தலாம்:
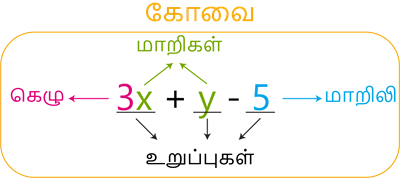
மாறி: தெரியாத மெய் எண்களைக் குறிக்க \(x\), \(y\), \(a\), \(b\) மற்றும் பல எண்களைப் பயன்படுத்துக்கிறோம். இவை மாறிகள் என்றழைக்கப்படும். மாறுபடும் பல எண் மதிப்புகளைக் கொண்டது மாறி ஆகும்.
மாறிலிகள்: மாறாத எண் மதிப்பைக் கொண்டவை மாறிலிகள் ஆகும்.
உறுப்புகள்: ஓர் பல்லுறுப்புக் கோவையில் \(+\),\(-\) இணைக்கப்பட்ட பகுதிகள், அதன் உறுப்புகள் ஆகும் .
கெழுக்கள்: ஒரு பல்லுறுப்புக் கோவையில் ஒவ்வொரு உறுப்பிலும் மாறிகளின் பெருக்கல் காரணியே அதன் கெழு எனப்படும்.
பல்லுறுப்புக் கோவை இயற்கணித கோவையின் ஒரு வகை ஆகும்.
இங்கு பல்லுறுப்புக் கோவையின் கருத்துக்களைக் காணலாம்.
ஒரு பல்லுறுப்புக் கோவை என்பது மாறிகள் மற்றும் மாறிலிகளைக் கொண்டு நான்கு அடிப்படைச் செயல்களால் இணைக்கப்பட்ட தொகுப்பு ஆகும். இங்கு மாறிகளின் அடுக்கு குறையற்ற முழுக்கள் ஆகும்.
Example:
மேலேக் கொடுக்கப்பட்டுள்ள கோவை ஒரு பல்லுறுப்பு கோவை ஆகும். ஏனெனில் கொடுக்கப்பட்ட கோவையில் மாறி (\(x\)) மற்றும் மாறிலிகள் உள்ளன.மற்றும் உறுப்புகள் \(-\) , \(+\) ஆல் இணைக்கப்பட்டுள்ளன. மேலும், (\(x^{2}\) மற்றும் \(x\)) மாறிகளின் அடுக்கு ஓர் குறையற்ற முழு எண் ஆகும்.
இங்கு, \(p(x)\) என்பது \(x\)ஆல் ஆன பல்லுறுப்பு கோவை ஆகும், \(x\) என்பது மாறி , \(x²\)ன் கெழு \(1\), \(x\)ன் கெழு \(-5\), மற்றும் \(9\) ஆனது மாறிலி ஆகும்.
Important!
பல்லுறுப்புக் கோவைகள் பொதுவாக , , எனக் குறிக்கப்படும்.
கீழேக் கொடுக்கப்பட்டுள்ள இயற்கணிதக் கோவைகள் பல்லுறுப்பு கோவைகளா என சரிபார்க்கலாம்.
1. \(x^{2} + 6x\)
இங்கு \(x^{2}\) மற்றும் \(6x\) ஆகியவை கூட்டல் செயல்பாடு மூலம் இணைக்கப்பட்டுள்ளதன, மேலும் \(x\)ன் அடுக்கானது ஒரு முழு எண் ஆகும்.
எனவே \(x^{2} + 6x\) என்ற கோவை ஒரு பல்லுறுப்புக் கோவை ஆகும்.
2. \(\frac{1}{x}\).
கொடுக்கப்பட்டக் கோவையின் தலைகீழி \(x^{-1}\).
இங்கு \(x\)-ன் அடுக்கானது ஒரு குறை எண்.
எனவே \(\frac{1}{x}\) என்ற கோவை பல்லுறுப்புக் கோவை அல்ல.
3. \(y^{3}-3x^{2}y+3xy^{2}+x^{3}\)
இங்கு \(y^{3}\), \(3x^{2}y\), \(3xy^{2}\) மற்றும் \(x^{3}\) என்ற உறுப்புகள் கூட்டல் மற்றும் கழித்தல் செயல்பாட்டால் இணைக்கப்பட்டுள்ளது.
மேலும், \(x\) மற்றும் \(y\) என்ற மாறிகளின் அடுக்குகள் முழு எண்கள் ஆகும்.
எனவே, \(y^{3}-3x^{2}y+3xy^{2}+x^{3}\) என்ற கோவை ஒரு பல்லுறுப்புக் கோவை ஆகும்
4. \(z^{3}-8\sqrt{z}\)
இங்கு \(z\)-ன் அடுக்கு \(\frac{1}{2}\). இது ஒரு முழு எண் அல்ல.
எனவே கொடுப்பட்ட கோவை பல்லுறுப்புக் கோவை அல்ல.
தினசரி வாழ்கையில் பல்லுறுப்புக் கோவையின் பயன்பாடு:
1. இயற்பியல், வேதியியல், பொறியியல், பொருளாதாரம் போன்ற பல துறைகளில் பல்லுறுப்புக் கோவை பயன்படுகிறது.
2. பல்லுறுப்புக் கோவைகளை வரைபடமாகக் குறிக்கலாம்.
Register for free to see more content