PDF chapter test TRY NOW
தேற்றம் III: ஓர் இணைகரத்தில் எதிர்க் கோணங்கள் சமம்.
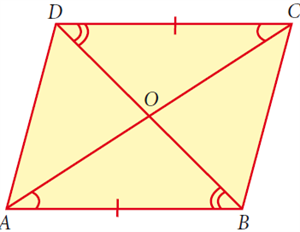
கொடுக்கப்பட்டவை: ஒரு இணைகரம் ABCD உடன் AC மற்றும் BD என்பன மூலைவெட்டிகள்.
நீரூப்பிக்க: ∠A = ∠C & ∠B = ∠D.
விளக்கம்: 'ஒரு இணைகரதின் எதிர்ரெதிர் பக்கங்கள் இணை மற்றும் சமம்'. So, AB||DC மற்றும் AD||BC.
எனவே, AB||DC யின் குறுக்குவெட்டி AC.
∠ACD = ∠CAB.
எனவே, AD||BC யின் குறுக்குவெட்டி AC.
∠DAC = ∠BCA.
இங்கு, \(∠A = ∠DAC+∠CAB = ∠BCA+∠ACD = ∠C\).
எனவே,AB||DC யின் குறுக்குவெட்டி BD.
∠CDB = ∠DBA.
எனவே, AD||BC யின் குறுக்குவெட்டி BD.
∠ADB = ∠DBC.
இங்கு, ∠B = DBA+∠DBC = ∠CDB+∠ADB = ∠D.
நிரூபிக்கப்பட்டது.
தேற்றம் IV: இணைகரத் தின் மூலைவிட்டங்கள் ஒன்றையொன்று இரு சமக் கூறிடும்.
கொடுக்கப்பட்டவை: ஒரு இணைகரம் ABCD உடன் AC மற்றும் BD என்பன மூலைவெட்டிகள் மற்றும் O என்ற புள்ளி AC மற்றும் BD சந்திக்கும் புள்ளி.
நிரூபிக்க: OA = OC மற்றும் OB = OD.
விளக்கம்: 'எதிர்ரெதிர் பக்கங்கள் இணை'. ஆகவே, AB||DC AD||BC.
எனவே AB||DC & AC என்பது குறுக்குவெட்டி.
∠ACD = ∠OCD = ∠CAB = ∠OAB (மாற்று உள் கோணங்கள் ...1)
அதுவே ∠OCD = ∠OAB.
எனவே AB||DC & BD என்பது குறுக்குவெட்டி.
∠BDC = ∠ODC = ∠DBA = ∠OBA (மாற்று உள் கோணங்கள் ...1)
அதுவே ∠ODC = ∠OBA.
இங்கு \Delta AOB & \Delta COD, இரு கோணங்கள் இணை (∠OCD = ∠OAB மற்றும் ∠ODC = ∠OBA) மற்றும் பக்கங்களின் அளவு சமம்.
கோ -ப-கோ விதியின் படி, இரு முக்கோணங்கள் \Delta AOB & \Delta COD சர்வசமம் எனில், அதன் பக்கங்கள் சமம்.
ஆகவே, OA = OC மற்றும் OB = OD (சர்வசம முக்கோணத்துடன் தொடர்புடையவை)
நிரூபிக்கப்பட்டது.
தேற்றம் V: ஒரே அடித்தளத்தையும் ஒரு சோடி இணைக்கோடுகளுக்கிடையேயும்அமையும் இணைகரங்களின் பரப்பளவுகள் சமம்.
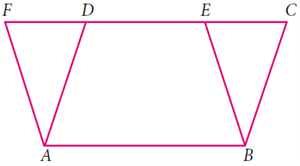
கொடுக்கப்பட்டவை: இரு இணைகரம் ABCD & ABEF யின் அடிதளம் AB &CF & AB என்பது இணைகோடுகள்.
நிரூபிக்க: ABCD இணைகரத்தின் பரப்பளவு = ABEF இணைகரத்தின் பரப்பளவு
விளக்கம்: இணைகரம் ABCD மற்றும் ABEF ஆனது AB என்ற பொதுப்பக்கத்தை உடையது.
இங்கு இரு ஜோடி முக்கோணங்கள் ADF மற்றும் BCE.
\angle ADF = \angle BCD மற்றும் \angle AFD \angle BEC.
AD = BC மற்றும் AF =BE (எதிர்ரெதிர் பக்கங்கள் சமம்).
இரு பக்கங்கள் மற்றும் இரு கோணங்கள் சமம்.
கோ-கோ-ப விதியின் படி, முக்கோணங்கள் ADF மற்றும் BCE என்பன சர்வசம முக்கோணங்கள்.
சர்வசம முக்கோணங்களின் பரப்பளவு சமம்.
ABCD இணைகரத்தின் பரப்பளவு = \Delta BCE யின் பரப்பளவு + ABED நாற்கரத்தின் பரப்பளவு.
= \Delta BCE இன் பரப்பளவு+ ABED நாற்கரத்தின் பரப்பளவு
= ABEF இணைகரத்தின் பரப்பளவு
ABCD இணைகரத்தின் பரப்பளவு = EFCD இணைகரத்தின் பரப்பளவு
நிரூபிக்கப்பட்டது.
இம்முறை மூலம் கீழ்கண்ட கிளைதேற்றங்கள் நிரூபிக்கப்பட்டுள்ளது.
Important!
கிளைதேற்றம் 1: ஒரு பொதுவான அடிப்பக்கத்தையும் ஒரு சோடி இணைகோடுகளுக்கு இடையேயும் அமையும் முக்கோணங்களின் பரப்பளவுகள் சமம்.
கிளைதேற்றம் 2: ஒரு பொதுவான அடிப்பக்கத்தையும் ஒரு சோடி இணைகோடுகளுக்கு இடையேயும் அமையும் ஒரு செவ்வகம் மற்றும் ஓர் இணைகரத்தின் பரப்பளவுகள் சமம்.
Register for free to see more content