PDF chapter test TRY NOW
தேற்றம் I: ஓர் இணைகரத்தின் எதிர்ப்பக்கங்கள் சமம்
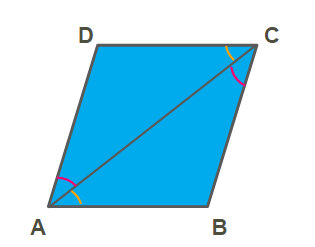
கொடுக்கப்பட்டவை: இணைகரம் \(ABCD\) உடன் \(AC\) என்பது குறுக்குவெட்டி.
நிரூபிக்க: \(\Delta ABC\cong\Delta ADC\).
விளக்கம்: இணைகரத்தில் 'இரண்டு ஜோடி எதிர் பக்கங்களும் ஒன்றுக்கொன்று இணை '. ஆகவே, \(AB||DC\) மற்றும் \(AD||BC\).
எனவே, \(AB||DC\) & \(AC\) என்பன குறுக்கு வெட்டி.
\(∠BAC =∠DCA\) (ஒன்றுவிட்ட கோணங்கள் ...1(மஞ்சள்)).
எனவே, \(AD||BC\) & \(AC\) என்பன குறுக்கு வெட்டி.
\(∠DAC =∠BCA\) (ஒன்றுவிட்ட கோணங்கள் ...2(சிகப்பு)).
இங்கு \(△ABC\) & \(△ ADC\).
\(∠BAC =∠DCA\) (எதிரெதிர் கோணங்களில் இருந்து ...1).
\(∠DAC =∠BCA\) (எதிரெதிர் கோணங்களில் இருந்து ...2).
\(AC=AC\) (பொதுப்பக்கம்).
\(கோ -ப- கோ\) விதியின் படி, இரு முக்கோணங்கள் சர்வசமம் எனில், அம்முக்கோணத்தின் பக்கங்கள் இணையாகும்.
எனவே, \(AB=CD\) & \(AD=BC\) (சர்வசம முக்கோணத்தின் படி).
நிரூபிக்கப்பட்டது.
தேற்றம் II: இணைகரத்தின் ஒரு மூலைவிட்டம் அதனை இரு சர்வசம முக்கோணங்களாகப் பிரிக்கின்றது.
நிரூபிக்க: \(ΔABC ≅ ΔADC\).
விளக்கம்: இணைகரத்தில் 'இரண்டு ஜோடி எதிர் பக்கங்களும் ஒன்றுக்கொன்று இணை '. ஆகவே, \(AB||DC\) மற்றும் \(AD||BC\).
எனவே \(AB||DC\) & \(AC\) என்பது குறுக்குவெட்டி.
\(∠BAC =∠DCA\) (ஒன்றுவிட்ட கோணங்கள் ...1(மஞ்சள்)).
எனவே \(AD||DC\) & \(AC\) என்பது குறுக்குவெட்டி.
\(∠DAC =∠BCA\) (ஓன்றுவிட்ட கோணங்கள் ...2(சிகப்பு)).
இங்கு \(△ABC\) & \(△ ADC\).
\(∠BAC =∠DCA\) (ஓன்றுவிட்ட கோணங்கள் ...1).
\(∠DAC =∠BCA\) (ஓன்றுவிட்ட கோணங்கள் ...2).
மேற்கண்ட படத்தில் இருந்து:
\(∠BAC +∠BCA\) \(=\) \(∠DAC + ∠DCA\)…(1)
முக்கோணங்களின் கோணங்களின் கூடுதல் படி \(ABC\).
\(∠B+∠BAC+∠BCA =180°\)…(2)
முக்கோணங்களின் கோணங்களின் கூடுதல் படி \(ACD\).
\(∠D+∠DAC+∠DCA=180°\)…(3)
(2) மற்றும் (3) யை (1) உடன் ஒப்பிட:
\(∠B = ∠D\).
தேற்றம் I, \(AB=CD\) & \(AD=BC\).
\(ப-கோ -ப\) விதியின் படி, இரு முக்கோணங்கள் \(ABC\) மற்றும் \(ADC\) சர்வசமம்.
Register for free to see more content