PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoநாண் மையத்தில் தாங்கும் கோணம்:
கற்பனையாக:
\(O\) வை மையமாக கொண்ட வட்டம் மற்றும் இரண்டு சமமான நாண்கள் \(PQ\) மற்றும் \(RS\).
\(PQ\) மற்றும் \(RS\) என்ற நாணின் இருமுனைகளை \(O\) என்ற மையத்துடன் இணைக்க.
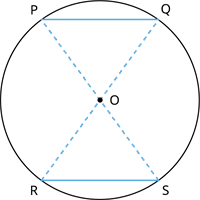
இரு முக்கோணங்கள் \(OPQ\) மற்றும் \(ORS\) உடன் சமமான பக்கங்கள் \(PQ\) மற்றும் \(RS\) (நாண்கள் சம நீளம் உடையவை.).
முக்கோணத்தின் மற்ற இரு கோணங்கள் சமம் மற்றும் அவை வட்டத்தின் ஆரங்கள் ஆகும்.
ப -ப -ப (பக்கம்-பக்கம்-பக்கம்) விதிப்படி, முக்கோணங்கள் \(OPQ\) மற்றும் \(ORS\) ஆகியன சர்வசமம்.
முக்கோணங்கள் சர்வசம எனில், கோணங்களின் அளவானது சமம்.
தேற்றத்தின் மறுதலை வட்ட மையத்தில் சம கோணங்களைத் தாங்கும் இரு நாண்கள்
தேற்றம்: வட்டத்தின் சம நாண்கள் வட்ட மையத்தில் இருந்து சம தொலைவில் இருக்கும்
விளக்கம்:
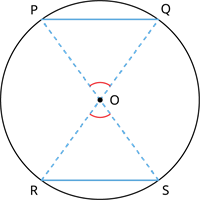
நாண்கள் \(PQ\) மற்றும் \(RS\) என்பன சமம், மையம் \(O\) வில் இருந்து நாண்கள் உண்டாகும் கோணங்கள் சமம் (i.e.) \(\angle POQ = \angle ROS\).
Example:
கோணம் \(x\) யைக் காண்க கொடுக்கப்பட்ட படத்தில் இருந்து நாண்கள் \(PQ\) மற்றும் \(RS\) என்பன சமம், மற்றும் \(O\) என்பது வட்டத்தின் மையம்.
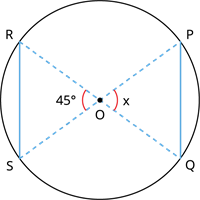
விளக்கம்:
மேற்கண்ட தேற்றத்தின் படி, நாண்கள் \(PQ\) மற்றும் \(RS\) ஆனது \(O\) வில் சம கோணத்தை ஏற்படுத்துகிறது.
\(\angle POQ = \angle ROS\).
இங்கு, \(\angle ROS = 45^{\circ}\).
ஆகவே, \(\angle POQ = 45^{\circ}\).
எனவே, கோணம் யின் அளவானது \(x = 45^{\circ}\).
கற்பனையாக:
மேற்கண்ட தேற்றத்தில் இருந்து, மையத்தில் இருந்து நாண்களின் நீளத்தைக் காண்க.
வட்டத்தின் மையம் \(O\) மற்றும் நாண்கள் \(PQ\) மற்றும் \(RS\).
\(PQ\) மற்றும் \(RS\) என்ற நாணின் முனைகள் \(Q\) மற்றும் \(R\) இணைக்க.
தேற்றத்தில் இருந்து \(\angle POQ = \angle ROS\).
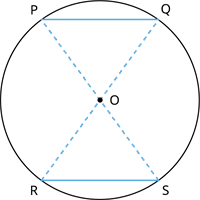
இரு முக்கோணங்களின் \(OPQ\) மற்றும் \(ORS\) மற்ற இரு பக்கங்கள் வட்டத்தின் ஆரங்கள் ஆகும்.
ப -கோ -ப (பக்கம்-கோணம்-பக்கம்) விதிப்படி, முக்கோணங்கள் \(OPQ\) மற்றும் \(ORS\) என்பன சர்வசமம்.
தேற்றத்தின் மறுதலை வட்ட மையத்திலிருந்து சம தொலைவில் உள்ள நாண்கள் சம
நீளமுள்ளவை..
தேற்றத்தின் மறுதலை : வட்ட மையத்திலிருந்து சம தொலைவில் உள்ள நாண்கள் சம
நீளமுள்ளவை.
விளக்கம் :
தேற்றத்தில் இருந்து, \(PQ\) மற்றும் \(RS\) என்ற இரு நாண்கள் மையம் \(O\) வில் இருந்து சம கோணத்தை உண்டாக்குகின்றன எனில் , நாண்கள் \(PQ\) மற்றும் \(RS\)சமம் (i.e.) \(PQ = RS\).
Example:
மையத்தில் இருந்து இரு நாண்கள் சமகோணத்தை உண்டாக்குகின்றன எனில், நாண்கள் சம நீளம் உடையவை என நிரூபிக்க.
விளக்கம்:
கொடுக்கப்பட்டவை, மையத்தில் இருந்து இரு நாண்கள் சமகோணத்தை உண்டாக்குகின்றன.
தேற்றத்தின் படி, வட்ட மையத்திலிருந்து சம தொலைவில் உள்ள நாண்கள் சம நீளமுள்ளவை.
இரு இணை நாண்கள் சமநீளம் உடையவை.
நிரூபிக்கப்பட்டது.
Register for free to see more content