PDF chapter test TRY NOW
நாணிற்கு மையத்திலிருந்து வரையப்படும் செங்குத்து:
கற்பனையாக:
Oவை மையமாக கொண்ட வட்டத்தின் PQ ஐ எடுத்துக்கொள்வோம்:
OR க்கு செங்குத்தாக PQ யை வரைக.
OP மற்றும் OQ வை இணைக்க.
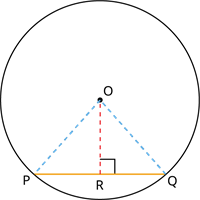
இரு செங்கோண முக்கோணங்கள் ORP மற்றும் ORQ, இதிலிருந்து \angle ORP = \angle ORQ = 90^{\circ} எனவே OR \perp PQ.
இங்கு, OP மற்றும் OQ என்பன ஆரங்கள். அவை, சம அளவுடையவை.
மேலும், முக்கோணம் ORP மற்றும் ORQ க்கு OR ஆனது பொதுப்பக்கம்.
சர்வசம முக்கோணத்தின் பண்பின் படி,
அதுவே PR = RQ.
இந்த விவாதத்தின் மூலம்
நாம் பின்வரும் முடிவைப் பெறுகிறோம்..
தேற்றம்: ஒரு வட்டத்தின் மையத்திலிருந்து ஒரு நாணிற்கு வரையப்படும் செங்குத்து அந்த
நாணை இருசமக் கூறிடும். .
விளக்கம்:
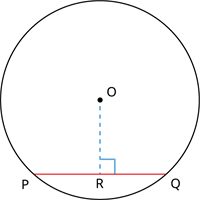
தேற்றத்தில் இருந்து O என்பது மையம் மற்றும் PQ என்பது நாண், O வில் இருந்து PQ என்ற நாணிற்கு (OR\) செங்குத்து மேலும் PQ யை இரு சம கூரிடும். (i.e.) PR = RQ.
Example:
வட்டத்தின் மையத்தில் இருந்து நாணின் நீளம் 24 செ.மீ செங்குத்தாக 9 செ.மீ. வட்டத்தின் ஆரம் காண்க.
விடை:
கொடுக்கப்பட்டவை:
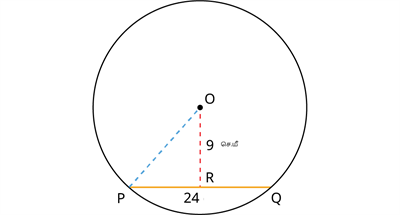
மையத்தில் இருந்து நாணின் தொலைவு = 9 செ.மீ
நாணின் நீளம் = 24 செ. மீ.
இங்கு, \angle ORP = 90^{\circ}.
தேற்றத்தின் படி:
PR = RQ
=
= 12 cm
முக்கோணம் OPR இல் இருந்து:
பிதாகரஸ் தேற்றத்தின் படி:
\text{கர்ணம்}^{2} = \text{அடுத்துள்ள பக்கம்}^{2} + \text{எதிர்ப்பக்கம்}^{2}
OP யின் நீளம் காண்க:
OP^{2} = OR^{2} + RP^{2}
= 9^{2} + 12^{2}
= 81 + 144
= 225
அதுவே, OP = \sqrt{225}
= 15 செ.மீ
எனவே, வட்டத்தின் ஆரம் 15 செ.மீ.
தேற்றம் 7 இன் மறுதலை :ஒரு வட்டத்தின் மையத்தையும் ஒரு நாணின் நடுப்புள்ளியையும்
இணைக்கும் கோடு அந்த நாணிற்குச் செங்குத்தாகும்.
விளக்கம்:
தேற்றத்தில் இருந்து O என்பது மையம் மற்றும் PQ என்பது நாண், O வில் இருந்து PQ என்ற நாணிற்கு (OR\) செங்குத்து மேலும் PQ யை இரு சம கூரிடும்.
Example:
ஒரு வட்டத்தின் மையத்தையும் ஒரு நாணின் நடுப்புள்ளியையும் இணைக்கும் கோடு அந்த நாணிற்குச் செங்குத்தாகும் எனில் அவற்றிற்கு இடைப்பட்ட கோணத்தைக் காண்க.
விடை:
தேற்றத்தின் படி, ஒரு வட்டத்தின் மையத்தையும் ஒரு நாணின் நடுப்புள்ளியையும் இணைக்கும் கோடு அந்த நாணிற்குச் செங்குத்தாகும்..
வட்டத்தின் மையத்தில் இருந்து வரையப்படும் கோடு மற்றும் மையப்புள்ளி, நாண் ஆகியவை ஒன்றுக்கொன்று செங்குத்தாகும்.
நாணின் மையத்தில் இருந்து மையத்திற்கு வரையப்படும் கோட்டின் கோணம் 90^{\circ}.
எனவே, ஒரு வட்டத்தின் மையத்தையும் ஒரு நாணின் நடுப்புள்ளியையும் இணைக்கும் கோடு அந்த நாணிற்குச் 90^{\circ}.
Register for free to see more content