PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமையம் மற்றும் பரிதியில் அமையும் கோணங்கள்:
கற்பனையாக:
வட்டத்தின் மையம் \(O\) மற்றும் மூன்று புள்ளிகள் \(P\), \(Q\) மற்றும் \(R\) வட்டத்தின் பரப்பளவின் மீது என்ற கோணம் \(\angle QOR\) மையம் \(O\) இல் இருந்தும் \(\angle QPR\) வட்டத்தின் பரப்பளவில் இருக்கிறது.
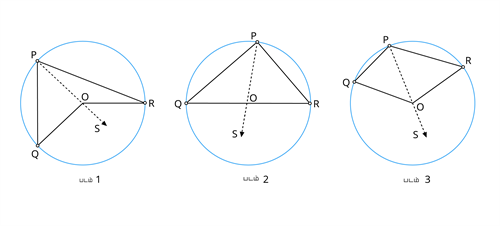
மூன்று வழிகள் (i) படம் \(1\) சிறிய பரிதி (ii) படம் \(2\) அரைவட்டம் மற்றும் (iii) படம் \(3\) பெரிய பரிதி.
மூன்று வழிகளில், மையத்தில் இருந்து \(\angle QOR\) யை ஏற்படுத்துகிறது மற்றும் \(\angle QPR\) என்பது \(P\) என்ற வட்டத்தின் பரப்பளவின் மீது உள்ளது.
\(PO\) வை \(S\) வரை விரிவுப்படுத்துக மற்றும் \(PS\) இணைக்க.
முக்கோணம் \(POQ\), \(\angle QOS\) என்பது வெளிகோணம்.
முக்கோண விதிப்படி, முக்கோணங்களின் வெளிகோணங்களின் கூடுதல் உள் எதிர் கோணங்களின் கூடுதலுக்கு சமம்.
அதுவே, \(\angle QOS\) \(=\) \(\angle OPQ\) \(+\) \(\angle PQO\).
இங்கு, \(OP\) \(=\) \(OQ\). ஆரங்கள் சமம்.
\(\angle OPQ\) \(=\) \(\angle PQO\) இரு சம முக்கோணத்தின் கோணங்களின் படி \(POQ\).
எனவே, \(\angle QOS\) \(=\) \(\angle OPQ\) \(+\) \(\angle OPQ\)
\(=\) \(2 \angle OPQ\) \(……\) \(\text{சமன்பாடு}(1)\)
முக்கோணம் \(POR\), \(\angle ROS\) என்பது வெளிகோணம்.
முக்கோண விதிப்படி, முக்கோணங்களின் வெளிகோணங்களின் கூடுதல் உள் எதிர் கோணங்களின் கூடுதலுக்கு சமம்.
அதுவே, \(\angle ROS\) \(=\) \(\angle OPR\) \(+\) \(\angle PRO\).
இங்கு, \(OP\) \(=\) \(OR\). ஆரங்கள் சமம்.
\(\angle OPR\) \(=\) \(\angle PRO\) இரு சம முக்கோணத்தின் கோணங்களின் படி \(POR\).
எனவே, \(\angle ROS\) \(=\) \(\angle OPR\) \(+\) \(\angle OPR\)
\(=\) \(2 \angle OPR\) \(……\) \(\text{சமன்பாடு}(2)\)
சமன்பாடுகள் \((1)\) மற்றும் \((2)\) இல் இருந்து:
\(\angle QOS\) \(+\) \(\angle ROS\) \(=\) \(2 \angle OPQ\) \(+\) \(2 \angle OPR\)
\(\angle QOR\) \(=\) \(2 (\angle OPQ + \angle OPR)\)
\(\angle QOR = 2\angle QPR\)
இதிலிருந்து பின்வரும் முடிவைப் பெறுகின்றோம்.
தேற்றம் : ஒரு வட்டவில் மையத்தில் தாங்கும் கோணம் அந்த வில்லை தவிர்த்து வட்டத்தின மீதிப் பரிதியில் ஏதேனும் ஒரு புள்ளியில் ஏற்படுத்தும் கோணத்தைப் போல் இரு மடங்காகும்.
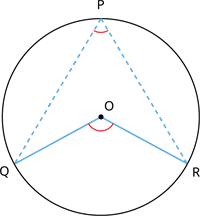
தேற்றத்தின் படி வட்டத்தின் மையம் \(O\)வில் இருந்து பரிதியால் ஏற்படுத்தும் கோணம் இருந்து இருமடங்காகும் புள்ளி \(P\)வரை வட்டத்தின் மறு பகுதி. (i.e.) \(\angle QOR = 2\angle QPR\).
Example:
கோணம் \(x\) யைக் காண்க. படத்தில் இருந்து பரிதியால் மையம் \(O\) ஏற்படுத்தும் கோணம் \(160^{\circ}\).
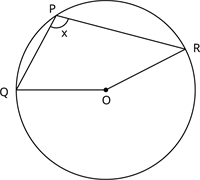
விளக்கம்:
தேற்றத்தின் படி, \(\angle QOR = 2\angle QPR\).
அதுவே, \(\angle QPR = \frac{1}{2} \மடங்கு \angle QOR\)
\(x = \frac{160^{\circ}}{2}\)
\(=\) \(80^{\circ}\)
கோணம் \(x\) ஆனது \(80^{\circ}\).
Register for free to see more content