PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoயூகம் 1
கற்பனையாக:
வட்ட மையம் O மற்றும் விட்டம் QR.
புள்ளி P யை வட்டத்தின் மீது குறிப்பிடுக.
வட்டத்தின் விட்டத்தின் அளவு 180^{\circ}.
பரிதி மையம் O ஏற்படுத்தும் கோணம் \angle QOR = 180^{\circ} மற்றும் \angle QPR வட்டத்தின் மேற்பரப்பில் உள்ளது.
தேற்றத்தின் படி, ஒரு வட்டவில் மையத்தில் தாங்கும் கோணம் அந்த வில்லைத் தவிர்த்து வட்டத்தின் மீதிப் பரிதியில் ஏற்படுத்தும் கோணத்தைப் போல் இரு மடங்காகும்.
ஆகவே, \angle QOR = 2\angle QPR.
\angle QPR = \frac{1}{2} \மடங்கு \angle QOR
= \frac{180^{\circ}}{2}
= 90^{\circ}
இதிலிருந்து பின்வரும் முடிவைப் பெறுகின்றோம்.
ஓர் அரைவட்டத்தில் அமையும் கோணம் செங்கோணம் ஆகும்.
விளக்கம்:
ஓர் வட்டத்தின் உள்ள கோணம் செங்கோணம் 90^{\circ}. விட்டத்தில் அமையும் கோணம் 90^{\circ}.
Example:
வட்டத்தின் மீது கோணத்தை ஏற்படுத்தும் பெரிய நாணின் நீளத்தைக் காண்க.
விடை:
ஒரு வட்டத்தின் பெரிய நாண் விட்டம் ஆகும்.
ஒரு வட்டத்தின் விட்டமானது ஏற்படுத்தும் கோணம் அதன் அரைவட்டத்தில் அமையும் கோணத்திற்கு சமம்.
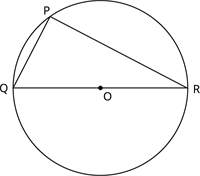
QR என்பது விட்டம் மற்றும் P என்பது வட்டத்தின் ஒரு புள்ளி.
ஒரு அரைவட்டத்தில் அமையும் கோணம் செங்கோணம் ஆகும்.
அதுவே, \angle QPR = 90^{\circ}.
வட்டத்தின் மீது கோணத்தை ஏற்படுத்தும் பெரிய நாணின் நீளத்தைக் காண்க.
90^{\circ}.
யூகம் 2
வட்டத்தின் சம பரிதிகள் மையத்தில் இருந்து சம கோணங்களை ஏற்படுத்துகிறது.
விளக்கம்:
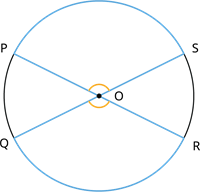
பரிதிகள் மற்றும் சமம் எனில், மையத்தில் இருந்து கோணங்கள் சமம். \angle POS = \angle QOR.
Example:
மற்றும் என்பன இரு சம பரிதிகள் மற்றும் ஒரு பரிதி மையத்தில் இருந்து ஏற்படுத்தும் கோணம் 60^{\circ} எனில், மற்றொரு பரிதி மையத்தில் இருந்து ஏற்படுத்தும் கோணத்தைக் காண்க.
விடை:
வட்டத்தின் சம பரிதிகள் மையத்தில் இருந்து சம கோணங்களை ஏற்படுத்துகிறது.
எனவே மற்றொரு பரிதி மையத்தில் இருந்து ஏற்படுத்தும் கோணத்தின் அளவானது 60^{\circ}.
Register for free to see more content