PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoபிரபஞ்ச இயக்கத்தின் அளவீட்டுக் கலையைத் துல்லியமாக முன்மொழிந்து விளக்கும் பகுதியே வடிவியல்
- சர் ஐசக் நியூட்டன்.
- சர் ஐசக் நியூட்டன்.
ஆயத்தொலை வடிவியல் என்ற கருத்து எப்படி உருவானதென்று உங்களுக்கு தெரியுமா?
ரெனே டேகார்ட் (Rene Descartes) ஒரு புகழ்பெற்ற பிரெஞ்சு கணிதவியலாளர் .
ஒரு நாள் ரெனே மிகவும் நோய்வாய்ப்பட்டார். அவர் படுக்கையில் ஓய்வெடுத்துக் கொண்டிருந்தபோது, மேற்கூரையைச் சுற்றி ஒரு பூச்சி பறப்பதைக் கண்டார் மற்றும் கூரையின் பல இடங்களில் அப்பூச்சி அமர்ந்தது. பூச்சி உட்காரும் எல்லா இடங்களையும் அறிய விரும்பினார். எனவே, அவர் காகிதத்தில் கிடைமட்ட மற்றும் செங்குத்து கோடுகளை வரைந்தார், இது மேற்கூரையைக் குறிக்கிறது.
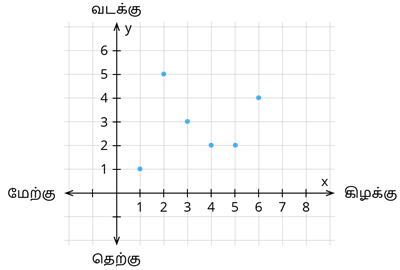
இந்த புள்ளிகள் பூச்சி மேற்கூரையில் அமர்ந்திருக்கும் இடங்களைக் குறிக்கின்றன. அவர் வடக்கு, தெற்கு, கிழக்கு மற்றும் மேற்கு திசைகளில் திசை மற்றும் பூச்சியின் இயக்கத்தைப் பயன்படுத்தி புள்ளிகளை வரைந்தார். பின்னர், அவர் அந்த இடத்தை \((x,y)\) என்று அழைத்தார், அங்கு \(x\) என்பது கிடைமட்ட திசையையும் (கிழக்கு மற்றும் மேற்கு திசை) மற்றும் \(y\) செங்குத்து திசையையும் (வடக்கு மற்றும் தெற்கு திசை) குறிக்கிறது. ஆயத்தொலை வடிவவியல் இப்படித்தான் உருவானது.
\(1637\)-இல் ரானே டெஸ்கார்ட்ஸ் "la geometric" என்ற புத்தகத்தை வெளியிட்டார், அவர் தனது புத்தகத்தில் ஒரு புதிய கருத்தை வழங்கினார், ஒவ்வொரு புள்ளியும் ஒரு மெய் எண்ணாலான வரிசைப்படுத்தப்பட்ட ஜோடியாக வெளிப்படுத்தப்படுகிறது. இது \((x, y)\) என்று அழைக்கப்படுகிறது.
ஒரு புள்ளியின் நிலையை ஒரு வரியைப் பொறுத்து விவரிப்பது ஒரு எண் கோட்டின் விஷயத்தில் எளிதானது. ஆனால் சில சூழ்நிலைகளில் ஒன்றுக்கு மேற்பட்ட வரிகளைப் பொறுத்து ஒரு புள்ளியின் நிலையை நாம் விவரிக்க வேண்டியிருக்கும்.
இதை ஒரு உதாரணத்தின் மூலம் அறிந்து கொள்ளலாம்,
உங்கள் அறையின் மேசை மீதுள்ள ஒரு கொட்டைவடி நீர் கோப்பையை மற்றொரு நபருக்கு அடையாளம் காண்பிக்கும்படி விவரிக்கவும். இது போல் இருக்கலாம்.
கொட்டைவடி நீர் கோப்பையை ஒரு புள்ளியாகவும், மேசையை ஒரு தளமாகவும் கருதுவோம். மேசையின் எந்த இரண்டு செங்குத்து விளிம்புகளையும் தேர்வு செய்யவும்.
நீண்ட விளிம்பிலிருந்து கோப்பையின் தூரத்தை அளவிடவும், அது \(30 \text{செ.மீ.}\) தூரத்தில் உள்ளது. மீண்டும், குறுகிய விளிம்பில் இருந்து கோப்பையின் தூரத்தை அளவிடவும், அது \(15\) \(\text{செ.மீ.}\) இதை நீங்கள் \(x\) மற்றும் \(y\) அச்சின் வரிசையைப் பொறுத்து கோப்பையின் நிலையை \((15, 30)\) அல்லது \((30, 15)\) என குறிப்பிடலாம்.
மேலே குறிப்பிட்டதிலிருந்து, ஒரு தளத்தில் இருக்கும் எந்தவொரு பொருளின் நிலையும் இரண்டு செங்குத்து கோடுகளை வைத்து குறிப்பிடப்படலாம் என்பதை நாம் தெரிந்துகொண்டோம்.
இந்த எளிய யோசனை தொலைநோக்கு விளைவுகளை ஏற்படுத்துகிறது, மேலும் கணிதத்தின் மிக முக்கியமான கிளையான ஆயத்தொலை வடிவியலை உருவாக்கியுள்ளது.
Reference:
https://en.wikipedia.org/wiki/Ren%C3%A9_Descartes#/media/File:Frans_Hals_-_Portret_van_Ren%C3%A9_Descartes.jpg
Frans Hals drew the portrait of Rene Descartes.
Register for free to see more content