PDF chapter test TRY NOW
எண்கோடு:
மேலே கொடுக்கப்பட்ட எண்கோட்டு வரிசையில், புள்ளி \(P\)இன் நிலையானது ஆதியிலிருந்து \(6\) அலகுகள் ஒரு புறத்தில் (கிடைமட்ட கோடு) குறிப்பிடப்படலாம்.
இவ்விதி எண் கோட்டின் எதிர்மறை பக்கத்திற்கும் பொருந்தும். ஒரு புள்ளியின் நிலையை ஒன்றுக்கு மேற்பட்ட இடங்களில் குறிப்பிடுவது சாத்தியமாகும்.
டேகார்ட் ஒரு தளத்தின்மேல் ஒன்றுக்கொன்று செங்குத்தான இரண்டு எண் கோடுகளை வைத்து மற்றும் இக்கோட்டில் உள்ள புள்ளிகளை குறிப்பிடுவதன் மூலம் தளத்திலுள்ள புள்ளிகளைக் கண்டறிவதற்கான வடிவமைப்பைக் கண்டுபிடித்தார்.
செங்குத்து கோடுகள் எந்த திசையில் வேண்டுமானாலும் இருக்கலாம். ஆனால், இந்த அத்தியாயத்தில் ஒரு தளத்தில் ஒரு புள்ளியைக் கண்டறிய இந்த இரண்டு வரிகளைத் தேர்ந்தெடுக்கும்போது, ஒரு வரி கிடைமட்டமாகவும், மற்றொன்று செங்குத்தாகவும் இருக்கும், கீழே உள்ளவாறு.
கார்ட்டீசியன் வடிவம்:
- இது இரு பரிமாண தளத்தில் உள்ள ஒரு புள்ளியின் நிலையை ஆய அச்சுத்தொலைவில் (\(x\)-அச்சு மற்றும் \(y\)-அச்சு) குறிப்பிடுவதாகும்.
- \(X'OX\) என்ற கிடைமட்ட எண் கோடு \(x\)-அச்சு எனப்படும்.
- \(Y'OY\) என்ற செங்குத்து எண் கோடு \(y\)-அச்சு எனப்படும்.
ஆயத் தொலை அச்சுக்கள்:
\(x\) ஆயத் தொலைவானது கிடை அச்சுத் தொலைவு எனவும், \(y\) ஆயத் தொலைவானது செங்குத்து அச்சுத் தொலைவு எனவும் குறிப்பிடப்படும். ஆயத் தொலை அச்சுகள் \((0,0)\) என்ற ஆதிப்புள்ளியில் வெட்டிக் கொள்ளும். இதை \(xy\) தளம் அல்லது கார்ட்டீசியன் தளம் அல்லது ஆயத் தொலை அச்சுக்கள் என்று அழைக்கப்படுகின்றது.
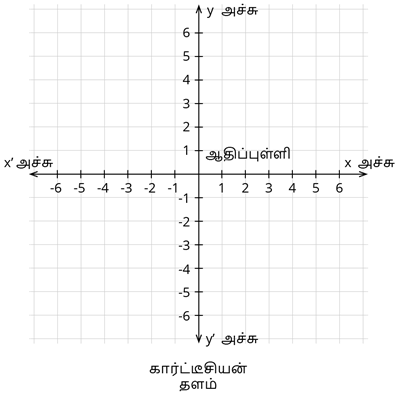
வரைபடத்திற்கான குறிகள்:
- \(x\) அச்சில் \(OX\) திசையில் உள்ள புள்ளி மிகை மற்றும் \(OX'\) திசையில் உள்ள புள்ளி குறை ஆகும்.
- \(y\) அச்சில் \(OY\) திசையில் உள்ள புள்ளி மிகை மற்றும் \(OY\) திசையில் உள்ள புள்ளி குறை ஆகும்.
Register for free to see more content