PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoமுக்கோணவியலின் விகிதங்களை பயன்படுத்தி \(\sin\), \(\cos\) மற்றும் \(\tan\) அவற்றின் தலைகீழிகளை பற்றி காண்போம்.
விகிதங்களின் தலைகீழிகள்:
\(\theta\) வை மையமாக கொண்ட செங்கோண முக்கோணத்தை காண்போம்.
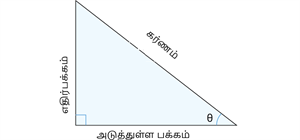
மூன்று அடிப்படை விகிதங்கள்:
- Sine
- Cosine
- Tangent
முக்கோணவியலின் தலைகீழிகள்.
| கோணங்களின் பெயர்கள் | Sine | Cosine | Tangent |
| கோணங்களின் சுருக்கிய வடிவம் | \(\sin\) | \(\cos\) | \(\tan\) |
| விகிதம் | \(\sin \theta\) \(=\) \(\frac{\text{எதிர்ப்பக்கம்}}{\text{கர்ணம்}}\) | \(\cos \theta\) \(=\) \(\frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}}\) | \(\tan \theta\) \(=\) \(\frac{\text{எதிர்பக்கம்}}{\text{அடுத்துள்ள பக்கம்}}\) |
| கோணங்களின் தலைகீழிகள் | Cosecant | Secant | Cotangent |
| தலைகீழிகளின் சுருக்கிய வடிவம் | \(\text{cosec}\) | \(\sec\) | \(\cot\) |
| ஒப்புமை அளவீடுகள் |  |  |  |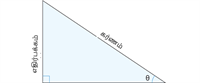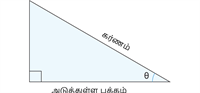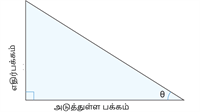
| தொடர்பு | \(\text{cosec}\,\theta\) \(=\) \(\frac{\text{கர்ணம்}}{\text{எதிர்பக்கம்}}\) | \(\sec \theta\) \(=\) \(\frac{\text{கர்ணம்}}{\text{அடுத்துள்ள பக்கம்}}\) | \(\cot \theta\) \(=\) \(\frac{\text{அடுத்துள்ள பக்கம்}}{\text{Oppos}}\) |
| அடிப்படை விகிதங்களுக்கு இடையே உள்ள தொடர்பு | \(\text{cosec}\,\theta\) \(=\) \(\frac{1}{\sin \theta}\) அல்லது \(\sin \theta\) \(=\) \(\frac{1}{\text{cosec}\,\theta}\) | \(\sec \theta\) \(=\) \(\frac{1}{\cos \theta}\) அல்லது \(\cos \theta\) \(=\) \(\frac{1}{\sec \theta}\) | \(\cot \theta\) \(=\) \(\frac{1}{\tan \theta}\) அல்லது \(\tan \theta\) \(=\) \(\frac{1}{\cot \theta}\) |
மேற்கண்ட விகிதங்களிலிருந்து கீழ்க்காணும் விகிதத் தொடர்புகளை நாம் அறியலாம்..
- தொடர்பு \(1\):
\(\text{cosec}\,\theta \times \sin \theta\) \(=\) \(\text{cosec}\,\theta \times \frac{1}{\text{cosec}\,\theta}\)
\(=\) \(1\)
எனவே, \(\text{cosec}\,\theta \cdot \sin \theta= 1\).
- தொடர்பு \(2\):
\(\sec \theta \times \cos \theta\) \(=\) \(\sec \theta \times \frac{1}{\sec \theta}\)
\(=\) \(1\)
எனவே, \(\sec \theta \cdot \cos \theta = 1\).
- தொடர்பு \(3\):
\(\cot \theta \times \tan \theta\) \(=\) \(\cot \theta \times \frac{1}{\cot \theta}\)
\(=\) \(1\)
எனவே, \(\cot \theta \cdot \tan \theta = 1\).
Register for free to see more content