PDF chapter test TRY NOW
முக்கோணவியல் என்பதின் ஆங்கிலச் சொல்லான Trigonometry என்பது கிரேக்கச் சொற்களான Trigonon-metron என்பவற்றிலிருந்து பெறப்பட்டுள்ளது. Trigonon-என்பதன் பொருள் முக்கோணம் என்பதாகும், மற்றும் metron - என்பதன் பொருள் அளவுகள் என்பதாகும்.
முக்கோணவியலின் விகிதங்கள்:
செங்கோண முக்கோணத்தில் இருந்து \(\theta\).
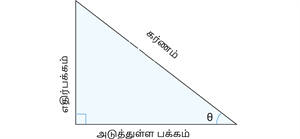
படத்தில் இருந்து \(\theta\) க்கு எதிரான பக்கம் எதிர்ப்பக்கம் ஆகும், \(\theta\) க்கு இணையான பக்கம் அடுத்துள்ளப் பக்கம் ஆகும், மற்றும் பெரிய பக்கம் கர்ணம் ஆகும்.
Important!
நினைவு கூறுக ! பிதாகர்ஸ் தேற்றத்தின் படி.
\(\theta\) வை மையமாக கொண்டு, செங்கோண முக்கோணத்தை ஏற்ப முக்கோணவியலின் மூன்று விகிதங்கள் உள்ளன .
அம்மூன்று விகிதங்களும் செங்கோண முக்கோணத்தின் ஒரு பக்கத்தை மற்றொரு பக்கத்தால் வகுக்கக் கிடைக்கும் விகிதங்களாகும்.
மூன்று அடிப்படை விகிதங்கள்:
- Sine
- Cosine
- Tangent
அவையாவன.
| கோணத்தின் பெயர் | Sine | Cosine | Tangent |
| சுருக்கிய வடிவம் | \(\sin\) | \(\cos\) | \(\tan\) |
| ஒப்புமை அளவீடுகள் |  |  |  |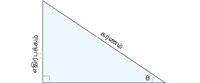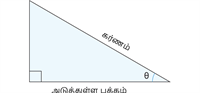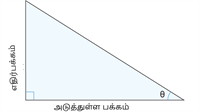
| விகிதம் | \(\sin \theta\) \(=\) \(\frac{\text{எதிர்பக்கம்}}{\text{கர்ணம்}}\) | \(\cos \theta\) \(=\) \(\frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}}\) | \(\tan \theta\) \(=\) \(\frac{\text{எதிர்பக்கம்}}{\text{அடுத்துள்ள பக்கம்}}\) |
Important!
1.முக்கோணவியல் விகிதங்களைக் குறிப்பிடும்போது பக்க அளவுகளின் விகிதங்களாகக் குறிப்பிடுவதால் அவை அலகுகளற்ற எண்களாகும்.
2. \(\sin \theta\), \(\cos \theta\) மற்றும் \(\tan \theta\) இது போன்ற விகிதங்களை \((\sin) \times (\theta)\), \((\cos) \times (\theta)\) மற்றும் \((\tan) \times (\theta)\) எனத்
தவறாக எடுத்துக் கொள்ளக்கூடாது.
தவறாக எடுத்துக் கொள்ளக்கூடாது.
Register for free to see more content