PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசமபக்க முக்கோணம் ABC யின் அளவுகள் 2 அலகுகள்.
அதுவே AB = BC = CA = 2 அலகுகள்.
கோண இருசம வெட்டி \angle A இல் சந்திக்கிறது BC ஆனது D இல் வெட்டுகிறது.
கோண இருசம வெட்டியானது சமபக்க முக்கோணத்தின் எதிர்பக்கத்தையும் வெட்டுகிறது.
அதுவே, BD = DC = 1 அலகுகள்.
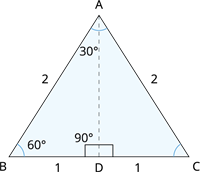
முதலில் கோணஇருசம வெட்டி BD யின் அளவினைக் காண்க.
முக்கோணம் ABD.
பிதாகரஸ் தேற்றத்தின் படி:
செங்கோண முக்கோணத்தில் , \text{கர்ணம்}^{2} = \text{அடுத்துள்ள பக்கம்}^{2} + \text{எதிர் பக்கம்}^{2}.
AB^2 = BD^2 + DA^2.
DA^2 = AB^2 - BD^2
DA^2 = 2^2 - 1^2
DA^2 = 4 - 1
DA^2 = 3
\Rightarrow DA = \sqrt{3}
செங்கோண முக்கோணத்தில் இருந்து:
| கோண அளவு 30^{\circ} | கோண அளவு 60^{\circ} |
| எதிர் பக்கம் = 1 அலகுகள் | எதிர் பக்கம் = \sqrt{3} அலகுகள் |
| அடுத்துள்ள பக்கம் = \sqrt{3} அலகுகள் | அடுத்துள்ள பக்கம் = 1 அலகுகள் |
| கர்ணம் = 2 அலகுகள் | கர்ணம் = 2 அலகுகள் |
முக்கோணவியல் விகிதங்கள் - கோண அளவு 30^{\circ} மற்றும் 60^{\circ}.
- Sine:
\sin 30^{\circ} | \sin 60^{\circ} |
\sin 30^{\circ} = \frac{\text{எதிர் பக்கம்}}{\text{கர்ணம்}} = \frac{1}{2} | \sin 60^{\circ} = \frac{\text{எதிர் பக்கம்}}{\text{கர்ணம்}} = \frac{\sqrt{3}}{2} |
- Cosine 30^{\circ}:
\cos 30^{\circ} | \cos 60^{\circ} |
\cos 30^{\circ} = \frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}} = \frac{\sqrt{3}}{2} | \cos 60^{\circ} = \frac{\text{அடுத்துள்ள பக்கம்}}{\text{கர்ணம்}} = \frac{1}{2} |
- Tangent:
\tan 30^{\circ} | \tan 60^{\circ} |
\tan 30^{\circ} = \frac{\text{எதிர் பக்கம்}}{\text{அடுத்துள்ள பக்கம்}} = \frac{1}{\sqrt{3}} | \tan 60^{\circ} = \frac{\text{எதிர் பக்கம்}}{\text{அடுத்துள்ள பக்கம்}} = \frac{\sqrt{3}}{1} = \sqrt{3} |
இவற்றை கொண்டு முக்கோணவியலின் தலைகீழிகள் காணலாம்:
- Cosecant:
\text{cosec}\,30^{\circ} | \text{cosec}\,60^{\circ} |
\text{cosec}\,30^{\circ} = \frac{1}{\sin 30^{\circ}} = \frac{2}{1} = 2 | \text{cosec}\,60^{\circ} = \frac{1}{\sin 60^{\circ}} = \frac{2}{\sqrt{3}} |
- Secant:
\sec 30^{\circ} | \sec 60^{\circ} |
\sec 30^{\circ} = \frac{1}{\cos 30^{\circ}} = \frac{2}{\sqrt{3}} | \sec 60^{\circ} = \frac{1}{\cos 60^{\circ}} = \frac{2}{1} = 2 |
- Cotangent:
\cot 30^{\circ} | \cot 60^{\circ} |
\cot 30^{\circ} = \frac{\text{1}}{\tan 30^{\circ}} = \frac{\sqrt{3}}{1} = \sqrt{3} | \cot 60^{\circ} = \frac{\text{1}}{\tan 60^{\circ}} = \frac{1}{\sqrt{3}} |
முக்கோணவியல் விகிதங்கள் - கோண அளவு 30^{\circ} மற்றும் 60^{\circ} கான அட்டவணை:
\sin \theta | \cos \theta | \tan \theta | \text{cosec}\,\theta | \sec \theta | \cot \theta | |
\theta = 30^{\circ} | \frac{1}{2} | \frac{\sqrt{3}}{2} | \frac{1}{\sqrt{3}} | 2 | \frac{2}{\sqrt{3}} | \sqrt{3} |
\theta = 60^{\circ} | \frac{\sqrt{3}}{2} | \frac{1}{2} | \sqrt{3} | \frac{2}{\sqrt{3}} | 2 | \frac{1}{\sqrt{3}} |
Register for free to see more content