PDF chapter test TRY NOW
Statement:
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Proof for the theorem:
Consider a circle with centre \(O\).
Let \(AB\) be the tangent to the circle at the point \(P\).
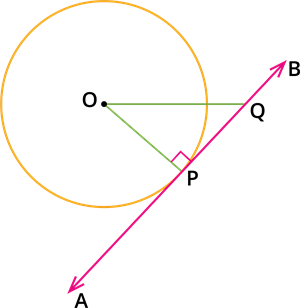
To prove:
The line \(OP\) is perpendicular to \(AB\).
Proof:
Take a point \(Q\) other than \(P\) on the tangent \(AB\) and join \(OQ\).
Here, \(Q\) must lie outside the circle.
Thus, \(OQ\) is longer than \(OP\).
That is \(OQ\) \(>\) \(OP\) at every point on \(AB\) except at \(P\).
Therefore, the point \(P\) is at the shortest distance from the centre \(O\).
We know that:
Out of all the line segments, drawn from a point to points of a line not passing through the point, the smallest is the perpendicular to the line.
By the theorem, \(OP\) is perpendicular to \(AB\).
Hence, the proof.
Example:
In the above given figure if \(OP\) \(=\) \(3\) \(cm\) and \(PQ\) \(=\) \(4\) \(cm\), find the length of \(OQ\).
Solution:
By the result, \(\angle OPQ\) \(=\) \(90^{\circ}\).
So, \(OPQ\) is a right angled triangle.
By the Pythagoras theorem, we have:
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
\(OQ^2\) \(=\) \(OP^2\) \(+\) \(PQ^2\)
\(OQ^2\) \(=\) \(3^2\) \(+\) \(4^2\)
\(OQ^2\) \(=\) \(9 + 16\)
\(OQ^2\) \(=\) \(25\)
\(\Rightarrow\) \(OQ\) \(=\) \(\sqrt{25}\)
\(OQ\) \(=\) \(5\)
Therefore, the measure of \(OQ\) \(=\) \(5\) \(cm\)
Important!
- By this theorem, we can say that at any point on the circle, there can be one and only one tangent.
- The line containing the radius through the point of contact is also called the normal to the circle at the point.
Register for free to see more content