UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us analyse the number of tangents drawn from a point on a circle in this article.
Case 1:
Consider a point O inside the circle.
Try to draw tangents to the circle through the point O.
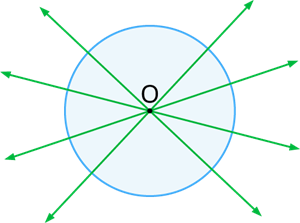
It is impossible to draw a tangent from a point inside the circle as every line intersects the circle at two points.
Therefore, no tangent can be drawn from an interior point of the circle.
Case 2:
Consider a point P on the circle.
Try to draw tangents to the circle through the point P.
It is possible to draw only one such tangent passing through the point P on the circle.
Therefore, only one tangent can be drawn at any point on a circle.
Case 3:
Consider a point P outside the circle.
Try to draw tangents to the circle through the point P.
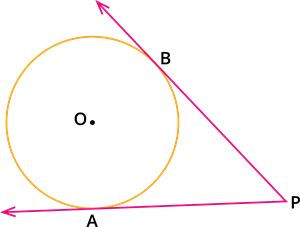
It is possible to draw exactly two tangents passing through the point P outside the circle.
Therefore, two tangents can be drawn from any exterior point of a circle.
The length of the segment of the tangent from the external point P and the point of contact A or B with the circle is called the length of the tangent from the point P to the circle.
Register for free to see more content