PDF chapter test TRY NOW
Based on the three basic trigonometric ratios \(\sin\), \(\cos\) and \(\tan\) we will define its reciprocals.
Reciprocal Ratios:
Consider a right-angled triangle with a corresponding angle \(\theta\).
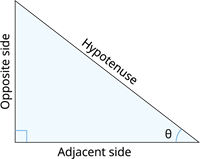
The three basic trigonometric ratios are:
- Sine
- Cosine
- Tangent
The table below depicts the relation of reciprocal ratios with the right-angled triangle.
| Name of the angle |
Sine
|
Cosine
|
Tangent
|
| Short form of the angle |
\(\sin\)
|
\(\cos\)
|
\(\tan\)
|
| Relationship |
\(\sin \theta\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
|
\(\cos \theta\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
|
\(\tan \theta\) \(=\) \(\frac{\text{Opposite side}}{\text{Adjacent side}}\)
|
| Name of the reciprocal angle |
Cosecant
|
Secant
|
Cotangent
|
| Short form of the angle |
\(\text{cosec}\)
|
\(\sec\)
|
\(\cot\)
|
| Measurements related to the right-angled triangle |
 |
 |
 |
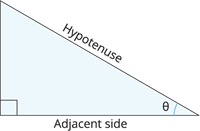| Relationship |
\(\text{cosec}\,\theta\) \(=\) \(\frac{\text{Hypotenuse}}{\text{Opposite side}}\)
|
\(\sec \theta\) \(=\) \(\frac{\text{Hypotenuse}}{\text{Adjacent side}}\)
|
\(\cot \theta\) \(=\) \(\frac{\text{Adjacent side}}{\text{Opposite side}}\)
|
| Relation with the basic ratio |
\(\text{cosec}\,\theta\) \(=\) \(\frac{1}{\sin \theta}\)
or
\(\sin \theta\) \(=\) \(\frac{1}{\text{cosec}\,\theta}\)
|
\(\sec \theta\) \(=\) \(\frac{1}{\cos \theta}\)
or
\(\cos \theta\) \(=\) \(\frac{1}{\sec \theta}\)
|
\(\cot \theta\) \(=\) \(\frac{1}{\tan \theta}\)
or
\(\tan \theta\) \(=\) \(\frac{1}{\cot \theta}\)
|
We can write certain identities based on these relationships.
- Identity \(1\):
\(\text{cosec}\,\theta \times \sin \theta\) \(=\) \(\text{cosec}\,\theta \times \frac{1}{\text{cosec}\,\theta}\)
\(=\) \(1\)
Therefore, \(\text{cosec}\,\theta \cdot \sin \theta= 1\).
- Identity \(2\):
\(\sec \theta \times \cos \theta\) \(=\) \(\sec \theta \times \frac{1}{\sec \theta}\)
\(=\) \(1\)
Therefore, \(\sec \theta \cdot \cos \theta = 1\).
- Identity \(3\):
\(\cot \theta \times \tan \theta\) \(=\) \(\cot \theta \times \frac{1}{\cot \theta}\)
\(=\) \(1\)
Therefore, \(\cot \theta \cdot \tan \theta = 1\).
Important!
The ratios of tangent and cotangent are also given by the following quotients:
- \(\tan \theta = \frac{\sin \theta}{\cos \theta}\) and
- \(\cot \theta = \frac{\cos \theta}{\sin \theta}\)
Register for free to see more content