UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreConsider an isosceles triangle \(ABC\) with angle measure \(45^{\circ}\) right-angled at \(B\).
Let the measure of the equal sides of the triangle be \(a\) units.
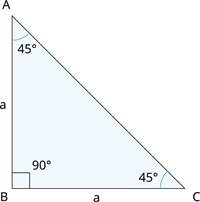
First, let us calculate the measure of the hypotenuse in the figure.
Since the given triangle is a right-angled triangle by the Pythagoras theorem, we have:
In a right angled triangle, \(\text{Hypotenuse}^{2} = \text{Adjacent side}^{2} + \text{Opposite side}^{2}\).
\(AC^2\) \(=\) \(AB^2\) \(+\) \(BC^2\).
\(AC^2\) \(=\) \(a^2\) \(+\) \(a^2\)
\(AC^2\) \(=\) \(2a^2\)
\(\Rightarrow AC\) \(=\) \(\sqrt{2a^2}\)
\(AC\) \(=\) \(a \sqrt{2}\) units
Therefore, for the given right-angled isosceles triangle we have:
Opposite side \(=\) \(a\) units
Adjacent side \(=\) \(a\) units
Hypotenuse \(=\) \(a \sqrt{2}\) units
Let us determine all the trigonometric ratios of \(45^{\circ}\).
- Sine \(45^{\circ}\):
\(\sin 45^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
\(=\) \(\frac{a}{a \sqrt{2}}\)
\(=\) \(\frac{1}{\sqrt{2}}\)
- Cosine \(45^{\circ}\):
\(\cos 45^{\circ}\) \(=\) \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
\(=\) \(\frac{a}{a \sqrt{2}}\)
\(=\) \(\frac{1}{\sqrt{2}}\)
- Tangent \(45^{\circ}\):
\(\tan 45^{\circ}\) \(=\) \(\frac{\text{Opposite side}}{\text{Adjacent side}}\)
\(=\) \(\frac{a}{a}\)
\(=\) \(1\)
Using these basic trigonometric ratios determine their reciprocals as follows:
- Cosecant \(45^{\circ}\):
\(\text{cosec}\,\theta\) \(=\) \(\frac{1}{\sin \theta}\)
\(=\) \(\sqrt{2}\)
- Secant \(45^{\circ}\):
\(\sec \theta\) \(=\) \(\frac{1}{\cos \theta}\)
\(=\) \(\sqrt{2}\)
- Cotangent \(45^{\circ}\):
\(\cot \theta\) \(=\) \(\frac{1}{\tan \theta}\)
\(=\) \(1\)
Let us summarize all the trigonometric ratios of \(45^{\circ}\) in the following table.
\(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) | \(\text{cosec}\,\theta\) | \(\sec \theta\) | \(\cot \theta\) | |
\(\theta = 45^{\circ}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{\sqrt{2}}\) | \(1\) | \(\sqrt{2}\) | \(\sqrt{2}\) | \(1\) |
Register for free to see more content