UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreWe will derive the trigonometric ratios of 0^{\circ} using the right angled triangle ABC.
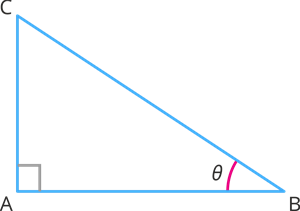
Let us now experiment with the given triangle concerning \angle B.
Reduce \theta to the extent it becomes zero.
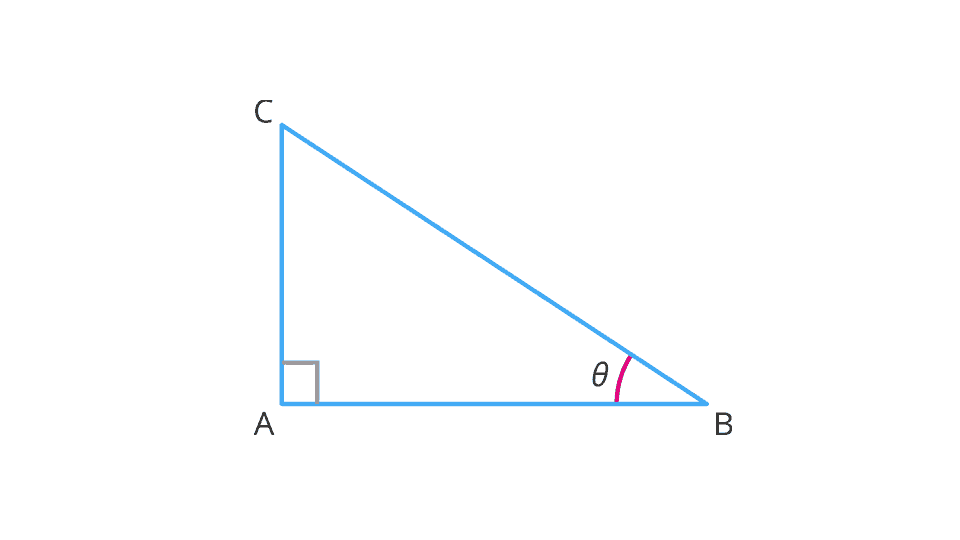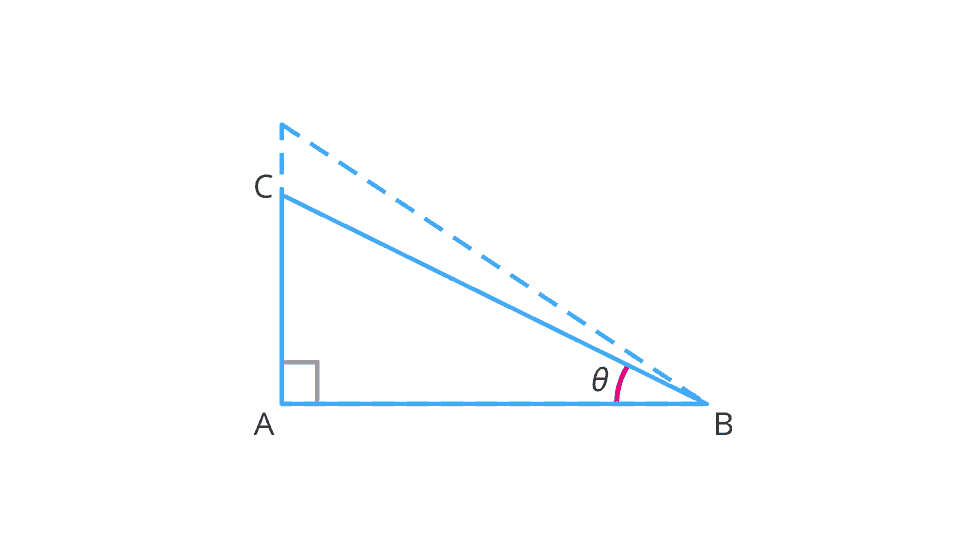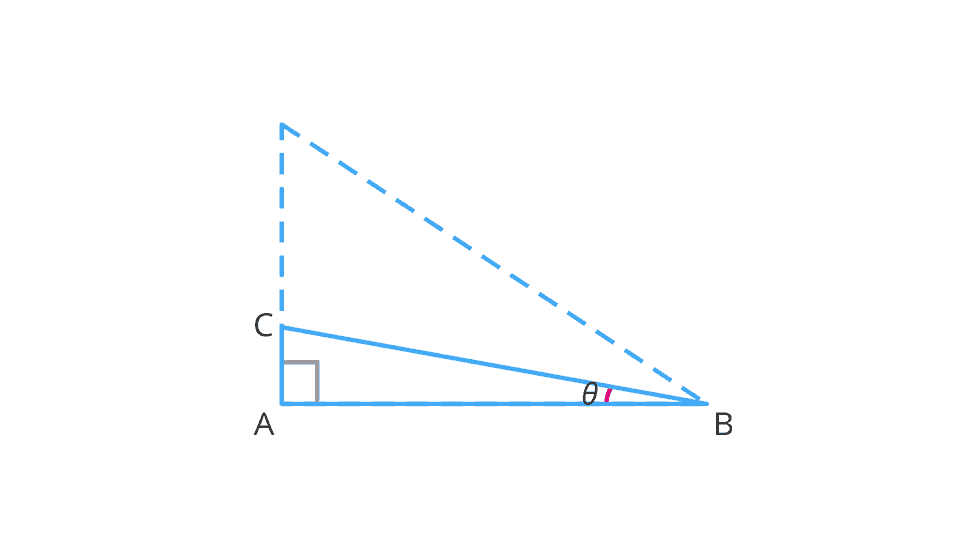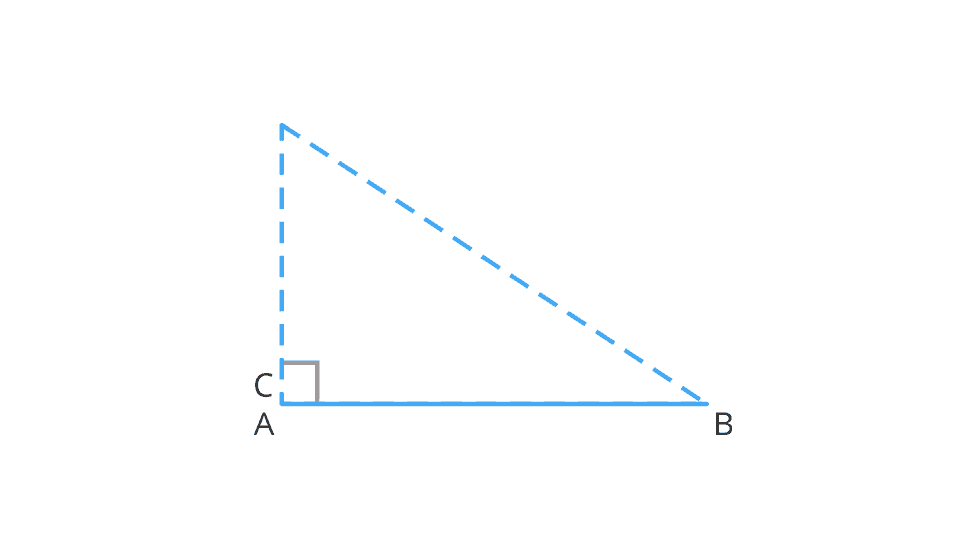
It is observed that as \angle B gets smaller and smaller, the point C gets closer to the point A.
That is, when \theta becomes very close to 0^{\circ}, the side BC becomes at most the same as the side AB.
This implies that the measure of AC becomes almost zero.
In the right angles triangle ABC we have:
Opposite side = AC
Adjacent side = AB
Hypotenuse = BC
Now, let us determine the trigonometric ratios when \theta = 0^{\circ} as follows.
- Sine 0^{\circ}:
\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}}
\sin \theta = \frac{AC}{BC}
\sin 0^{\circ} = \frac{0}{BC}
= 0
- Cosine 0^{\circ}:
\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}}
\cos \theta = \frac{AB}{BC}
\cos 0^{\circ}= 1 [When \angle B = 0^{\circ}, AB = BC]
- Tangent 0^{\circ}:
\tan 0^{\circ} = \frac{\sin 0^{\circ}}{\cos 0^{\circ}}
= \frac{0}{1}
= 0
Using these basic trigonometric ratios determine their reciprocals as follows:
- Cosecant 0^{\circ}:
\text{cosec}\,0^{\circ} = \frac{1}{\sin 0^{\circ}}
= \frac{1}{0}
= not defined
- Secant 0^{\circ}:
\sec 0^{\circ} = \frac{1}{\cos 0^{\circ}}
= \frac{1}{1}
= 1
- Cotangent 0^{\circ}:
\cot 0^{\circ} = \frac{1}{\tan 0^{\circ}}
= \frac{1}{0}
= not defined
Let us summarize all the trigonometric ratios of 0^{\circ} in the following table.
\sin \theta | \cos \theta | \tan \theta | \text{cosec}\,\theta | \sec \theta | \cot \theta | |
\theta = 0^{\circ} | 0 | 1 | 0 | not defined | 1 | not defined |
Register for free to see more content