Geometrical meaning of the zeroes of linear polynomial — lesson. Mathematics CBSE, Class 10.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Learn more

A polynomial of the form

$ax + b$ ,

$a \neq 0$ is a linear polynomial.

The graph of a linear polynomial is a straight line.

Consider the graph of

$y = 2x + 1$ .

$x$	$-2$	$-1$	$0$	$1$	$2$
$2x + 1$	$2(-2) + 1$ $=$ $- 4 + 1$ $=$ $-3$	$2(-1) + 1$ $=$ $- 2 + 1$ $=$ $-1$	$2(0) + 1$ $=$ $0 + 1$ $=$ $1$	$2(1) + 1$ $=$ $2 + 1$ $=$ $3$	$2(2) + 1$ $=$ $4 + 1$ $=$ $5$
$y$ $=$ $2x + 1$	$-3$	$-1$	$1$	$3$	$5$

Join the coordinates

$(-2, -3)$ ,

$(-1, -1)$ ,

$(0, 1)$ ,

$(1, 3)$ and

$(2, 5)$ by a straight line so as to obtain the graph of

$y = 2x + 1$ .

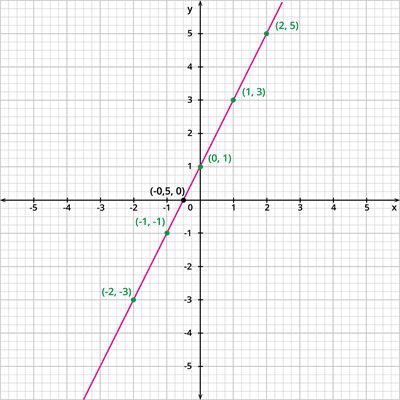It is observed that, the graph of the polynomial

$y = 2x + 1$ intersects the

$x$

$-$ axis at the point

$(- 0.5, 1)$ .

Also by the definition, the zero of

$y = 2x + 1$ is given by

$x = \frac{-1}{2} = -0.5$ .

Thus, we can say that the zero of a linear polynomial is the

$x$

$-$ coordinate of the point where the graph of the polynomial intersects the

$x$

$-$ axis.

In general, for a linear polynomial

$ax + b$ ,

$a \neq 0$ , the graph of

$y = ax + b$ represents a straight line which intersects the

$x$

$-$ axis exactly at the point

$\left(\frac{-b}{a}, 0\right)$ .

The linear polynomial

$ax + b$ ,

$a \neq 0$ , has exactly one zero namely

$\frac{-b}{a}$ which is the

$x$

$-$ coordinate of the point where the graph of the polynomial intersects the

$x$

$-$ axis.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

2. Geometrical meaning of the zeroes of linear polynomial

Theory: