PDF chapter test TRY NOW
A polynomial of the form ax^2 + bx + c, a \neq 0 is a quadratic polynomial.
The graph of a quadratic polynomial is a parabolic curve either open upwards or open downwards depending on whether a > 0 or a < 0.
Consider the graph of y = 2x^2 + 3x + 1.
x | -2 | -1 | 0 | 1 | 2 |
2x^2 | 2(-2)^2 = 2(4) = 8 | 2(-1)^2 = 2(1) = 2 | 2(0)^2 = 2(0) = 0 | 2(1)^2 = 2(1) = 2 | 2(2)^2 = 2(4) = 8 |
3x | 3 \times -2 = -6 | 3 \times -1 = -3 | 3 \times 0 = 0 | 3 \times 1 = 3 | 3 \times 2 = 6 |
2x^2 + 3x + 1 | 8 - 6 + 1 = 3 | 2 - 3 + 1 = 0 | 0 + 0 + 1 = 1 | 2 + 3 + 1 = 6 | 8 + 6 + 1 = 15 |
y = 2x^2 + 3x + 1 | 3 | 0 | 1 | 6 | 15 |
Join the coordinates (-2, 3), (-1, 0), (0, 1), (1, 6) and (2, 15) by a smooth curve so as to obtain the graph of y = 2x^2 + 3x + 1.
 |
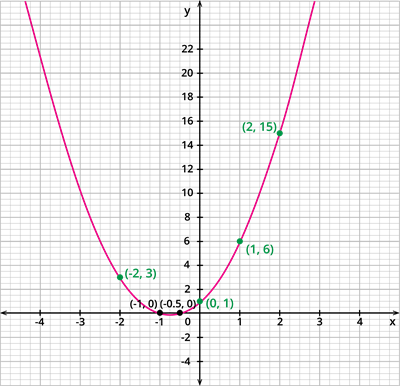It is observed that, the graph of the polynomial y = 2x^2 + 3x + 1 intersects the x - axis at the points (-1, 0) and (-0.5, 0).
Thus, we can say that the zero of a quadratic polynomial is the x - coordinates of the point where the graph of the polynomial intersects the x - axis.
Let us discuss few cases of graphs of a quadratic polynomial.
Case 1: The graph of the quadratic polynomial cuts the x - axis at two points, as shown below.
 |  |
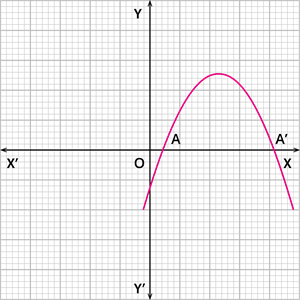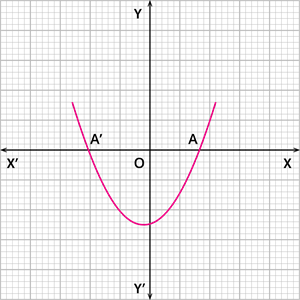In this case, the number of zeroes of the polynomial is 2.
Case 2: The graph of the quadratic polynomial cuts the x - axis at one point, as shown below.
 |  |
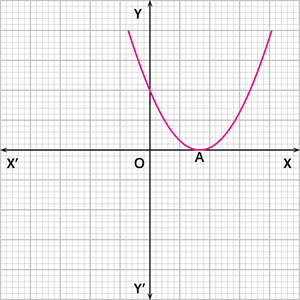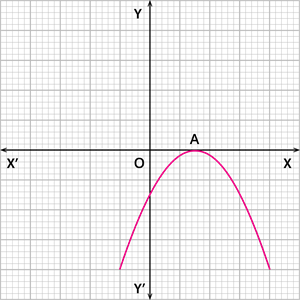In this case, the number of zeroes of the polynomial is 1.
Case 3: The graph of the quadratic polynomial does not intersect the x - axis at any point, as shown below.
 |  |
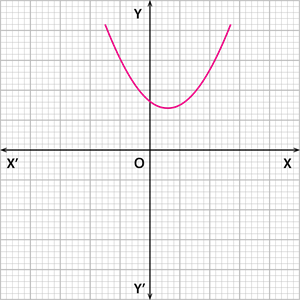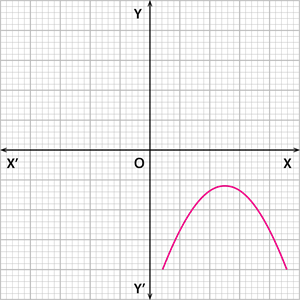In this case, the number of zeroes of the polynomial is 0.
The quadratic polynomial ax^2 + bx + c, a \neq 0, has at most two zeroes which is the x - coordinates of the point where the graph of the polynomial intersects the x - axis.
Register for free to see more content