UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreA polynomial of the form \(ax^3 + bx^2 + cx + d\), \(a \neq 0\) is a cubic polynomial.
Consider the graph of \(y = 2x^3 - 3x\).
\(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
\(2x^3\) | \(2(-2)^3\) \(=\) \(2(-8)\) \(=\) \(-16\) | \(2(-1)^3\) \(=\) \(2(-1)\) \(=\) \(-2\) | \(2(0)^3\) \(=\) \(2(0)\) \(=\) \(0\) | \(2(1)^3\) \(=\) \(2(1)\) \(=\) \(2\) | \(2(2)^3\) \(=\) \(2(8)\) \(=\) \(16\) |
\(3x\) | \(3 \times -2\) \(=\) \(-6\) | \(3 \times -1\) \(=\) \(-3\) | \(3 \times 0\) \(=\) \(0\) | \(3 \times 1\) \(=\) \(3\) | \(3 \times 2\) \(=\) \(6\) |
\(2x^2 - 3x\) | \(-16\) \(+\) \(6\) \(=\) \(-10\) | \(-2\) \(+\) \(3\) \(=\) \(1\) | \(0\) \(-\) \(0\) \(=\) \(0\) | \(2\) \(-\) \(3\) \(=\) \(-1\) | \(16\) \(-\) \(6\) \(=\) \(10\) |
\(y\) \(=\) \(2x^2 - 3x\) | \(-10\) | \(1\) | \(0\) | \(-1\) | \(10\) |
Join the coordinates \((-2, -10)\), \((-1, 1)\), \((0, 0)\), \((1, -1)\) and \((2, 10)\) by a smooth curve so as to obtain the graph of \(y = 2x^2 - 3x\).
 |
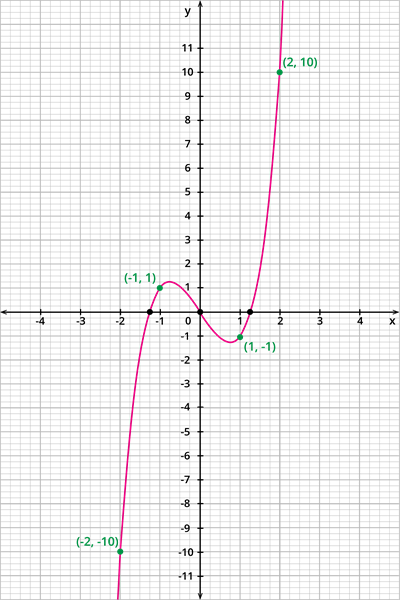It is observed that, the graph of the polynomial \(y = 2x^2 - 3x\) intersects the \(x\) \(-\) axis at three points.
Thus, we can say that the zero of a cubic polynomial is the \(x\) \(-\) coordinates of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
Let us discuss few cases of graphs of a cubic polynomial.
Case 1: The graph of the cubic polynomial cuts the \(x\) \(-\) axis at one point, as shown below.
 |
In this case, the number of zeroes of the polynomial is \(1\).
Case 2: The graph of the cubic polynomial cuts the \(x\) \(-\) axis at two points, as shown below.
 |
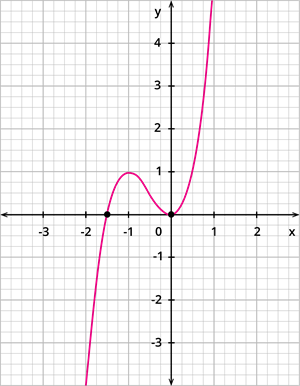In this case, the number of zeroes of the polynomial is \(2\).
Case 3: The graph of the cubic polynomial cuts the \(x\) \(-\) axis at three points, as shown below.
 |
In this case, the number of zeroes of the polynomial is \(3\).
The cubic polynomial \(ax^3 + bx^2 + cx + d\), \(a \neq 0\), has at most three zeroes which is the \(x\) \(-\) coordinates of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
Important!
In general, the graph of the polynomial of \(n\) degree intersects the \(x\) \(-\) axis at atmost \(n\) points.
In other words, the polynomial of \(n\) degree has atmost \(n\) zeroes.
Register for free to see more content