PDF chapter test TRY NOW
Monomials that have the like products of the variable terms, even if the terms' order is different, are called similar monomials.
Example:
Similar monomials are:
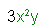 | and | 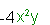 |
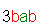 | and | 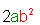 |
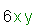 | and | 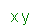 |
5 | and | -3 |
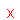 | and | 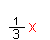 |
Non-similar monomials are, for example, 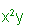 and
and 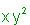 .
.
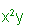 and
and 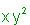 .
.If similar monomials have the like coefficients, then these monomials are called mutually equal monomials.
If the monomials are mutually equal, it can be verified when the monomials are written in the standard form.
Example:
Out of these monomials
mutually equal monomials are
.
This can be proved if all the monomials are written in the standard form:
If the coefficients of similar monomials are the opposite numbers, then these monomials are called the opposite monomials.
Example:
Out of these monomials
the opposite monomials are
