Angle sum property — lesson. Mathematics CBSE, Class 7.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Let's see the remarkable property that connects three angles of a triangle.

The sum of the measure of three angles of a triangle is 180°.

Example:

Consider a triangle

$ABC$ with interior angles measures

$∠1$ ,

$∠2$ and

$∠3$ . Draw a line

$DE$ parallel to

$BC$ .

Now the angle formed by the parallel line

$DE$ with the triangle

$ABC$ is

$∠4$ and

$∠5$ .

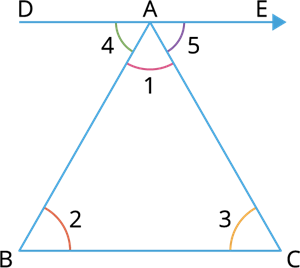
Since

$DE$ is parallel to

$BC$ , using the alternate interior angle property

$∠2$ must equal to

$∠4$ .

Similarly,

$∠3$ must be equal to

$∠5$ .

That is

$∠2 = ∠4$ and

$∠3 =∠5$ .

$DE$ is a straight line,

$∠5$ and

$∠CAD$ are linear pairs (Pair of adjacent supplementary angles).

$∠5 + ∠CAD = 180°$

That is,

$∠5 + ∠1 + ∠4 = 180°$

Equivalently,

$∠1 + ∠2 + ∠3 = 180°$ .

It states that the total measures of the three angles of a triangle is

$180°$ .

Did you find an error?

2. Angle sum property