PDF chapter test TRY NOW
In sixth century B.C., a Greek philosopher Pythagoras had done a amazing discovery over right triangle.
In a right-angled triangle, the sum of the square on the legs is equal to the square on the hypotenuse.
Let's us experiment the Pythagoras theorem.
Draw a right angled triangle \(ABC\).
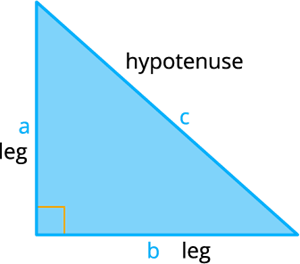
Here \(AB = a, BC = b\) and \(AC = c\).
The legs are \(AB\) and \(BC\). The hypotenuse is \(AC\).
Let's find the square of each side and verify the provided theorem.
As \(AB = a\), \(BC = b\) and \(AC = c\), the square of each side becomes \(a²\), \(b²\) and \(c²\).
If we draw this case in graph paper, it would give the result as area of the square with side length \(AC\) is equal to the sum of area of the square with side length \(AB\) and the area of square with side length \(BC\).
That is, square on the hypotenuse (\(c²\)) is equal to the sum of square on the legs (\(a²+b²\)).
Thus, \(a²+b²=c²\).
Important!
The converse of the Pythagoras theorem hold. This implies, 'if the Pythagoras property holds, the triangle must be right-angled triangle'.
Register for free to see more content