PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

9. Theorem on interior angles of a cyclic quadrilaterals

Cyclic Quadrilateral

A four-sided figure inscribed in a circle such that all its vertices lie on the circumference of the circle is said to be a cyclic quadrilateral.

Theorem: The sum of either pair of opposite angles of a cyclic quadrilateral is

$180^{\circ}$ .

Explanation:

The theorem states that the sum of the interior opposite angles of a cyclic quadrilateral is

$180^{\circ}$ .

That is,

$\angle A + \angle C = 180^{\circ}$ .

And

$\angle B + \angle D = 180^{\circ}$ .

Proof of the theorem:

Consider a quadrilateral

$ABCD$ whose vertices lie on the circumference of the circle with centre

$O$ .

Connect all the four vertices with centre

$O$ to get four isosceles triangle

$AOB$ ,

$BOC$ ,

$COD$ and

$DOA$ where the sides

$OA$ ,

$OB$ ,

$OC$ and

$OD$ are the radii.

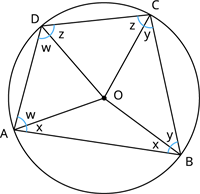
The sum of the angles around the centre of a circle is

$360^{\circ}$ .

Also, the sum of all the interior angles of a triangle is

$180^{\circ}$ .

Hence:

$\begin{array}{l} ∠ w + ∠ w + ∠ AOD = 180 ° \\ ∠ x + ∠ x + ∠ AOB = 180 ° \\ ∠ y + ∠ y + ∠ BOC = 180 ° \\ ∠ z + ∠ z + ∠ COD = 180 ° \end{array}$

Adding all the equations we have:

$2 (\angle w + \angle x + \angle y + \angle z) + \angle O = 4\times180^{\circ}$

$2 (\angle w + \angle x + \angle y + \angle z) + 360^{\circ} = 720^{\circ}$

$2 (\angle w + \angle x + \angle y + \angle z) = 720^{\circ} - 360^{\circ}$

$2 (\angle w + \angle x + \angle y + \angle z) = 360^{\circ}$

$\angle w + \angle x + \angle y + \angle z = 180^{\circ}$

This is rewritten as,

$\angle A + \angle C = 180^{\circ}$ .

Similarly,

$\angle B + \angle D = 180^{\circ}$ .

Example:

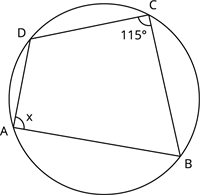
Find the unknown angle

$x$ in the given figure.

Solution:

By the theorem, opposite angles of a cyclic quadrilateral are supplementary.

This implies:

$\angle A + \angle C = 180^{\circ}$

$x + 115^{\circ} = 180^{\circ}$

$x = 180^{\circ} - 115^{\circ}$

$x = 65^{\circ}$

Converse of Theorem: If the sum of a pair of opposite angles of a quadrilateral is

$180^{\circ}$ , the quadrilateral is cyclic.

Explanation:

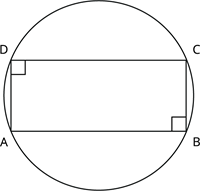
The theorem states that if the sum of the interior opposite angles of any quadrilateral is

$180^{\circ}$ , then that quadrilateral is said to be cyclic. Here, in the figure, the sum of the

$\angle A$ and

$\angle C$ is

$180^{\circ}$ .

$90^{\circ} + 90^{\circ} = 180^{\circ}$

Thus, the quadrilateral

$ABCD$ is cyclic.

Example:

Prove that a square inscribed in a circle is cyclic.

Proof:

Let

$ABCD$ be the square inscribed in a circle.

It is known that every angle of a square is

$90^{\circ}$ .

Here

$\angle A + \angle C = 90^{\circ} + 90^{\circ}$

Implies,

$\angle A + \angle C$

$=$

$180^{\circ}$

Similarly,

$\angle B + \angle D = 90^{\circ} + 90^{\circ}$

Implies,

$\angle B + \angle D$

$=$

$180^{\circ}$

According to the theorem, the pair of opposite angles of the square is supplementary.

Hence the square inscribed in a circle is cyclic.

Previous theory

Exit to the topic

Next exercise

Send feedback

Did you find an error?

Send it to us!

9. Theorem on interior angles of a cyclic quadrilaterals

Theory: