PDF chapter test TRY NOW
Theorem IV
In a parallelogram, opposite angles are equal.
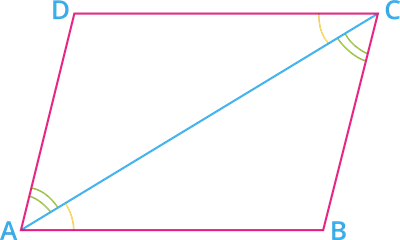
Given: ABCD is a parallelogram.
Construction: Join the diagonal AC.
To prove: \angle A = \angle C and \angle B = \angle D
Proof: We know that "opposite sides of a parallelogram are parallel".
AB \ || \ CD and BC \ || \ AD
Since AB \ || \ CD and AC is a transversal.
\angle BAC = \angle DCA [alternate interior angles] - - - - - (I)
Also, AD \ || \ BC and AC is a transversal.
\angle DAC = \angle BCA [alternate interior angles] - - - - - (II)
Add equations (I) and (II).
\angle BAC + \angle DAC = \angle DCA + \angle BCA
\angle BAD = \angle DCB
That is, \angle A = \angle C - - - - - - (III)
Now, join the diagonal BD.
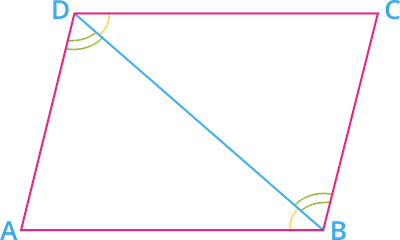
Since AB \ || \ CD and BD is a transversal.
\angle ABD = \angle CDB [alternate interior angles] - - - - - (IV)
Also, AD \ || \ BC and BD is a transversal.
\angle CBD = \angle ADB [alternate interior angles] - - - - - (V)
Add equations (IV) and (V).
\angle ABD + \angle CBD = \angle CDB + \angle ADB
\angle ABC = \angle ADC
That is, \angle B = \angle D - - - - - - (VI)
From (III) and (VI), we get:
The opposite angles of a parallelogram are equal.
Theorem V
If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.

Given: ABCD is a quadrilateral, where \angle A = \angle C and \angle B = \angle D.
To prove: ABCD is a parallelogram.
Proof: By angle sum property of a quadrilateral:
\angle A + \angle B + \angle C + \angle D = 360^\circ
\angle A + \angle B + \angle A + \angle B = 360^\circ (Using given)
2 \angle A + 2 \angle B = 360^\circ
2 ( \angle A + \angle B) = 360^\circ
\angle A + \angle B = 180^\circ - - - - (I)
Now, consider AB is the transversal for the lines AD and BC.
\angle A and \angle B are interior angles on the same side of transversal line AB.
"Two lines cut by a transversal are parallel if and only if sum of interior angles on the same side of the transversal are 180^\circ".
Since \angle A + \angle B = 180^\circ
\Rightarrow AD \ || \ BC - - - - - (II)
Similarly, \angle A + \angle B + \angle C + \angle D = 360^\circ
\angle A + \angle D + \angle A + \angle D = 360^\circ (Using given)
2 \angle A + 2 \angle D = 360^\circ
2 ( \angle A + \angle D) = 360^\circ
\angle A + \angle D = 180^\circ - - - - (III)
Similarly, AD is the transversal for lines AB and DC.
\angle A and \angle D are interior angles on the same side of transversal line AD.
"Two lines cut by a transversal are parallel if and only if sum of interior angles on the same side of the transversal are 180^\circ".
Since \angle A + \angle D = 180^\circ
\Rightarrow AB \ || \ DC - - - - - (IV)
From equations (II) and (IV), we get:
AD \ || \ BC and AB \ || \ DC
Both pair of opposite sides are parallel.
Therefore, ABCD is a parallelogram.
