PDF chapter test TRY NOW
Theorem IX
The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
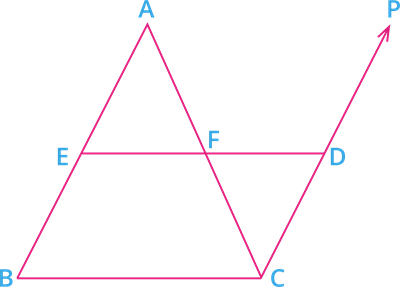
Given: ABC is a triangle, where E is the mid-point of AB and F is the mid-point of AC.
To prove: EF \ || \ BC
Construction: Draw a line segment through C parallel to AB and extend EF to meet this line at D.
Proof: Since E is the mid-point of AB, AE = EB - - - - (I)
Since F is the mid-point of AC, AF = FC - - - - (II)
By construction AB \ || \ CD.
\Rightarrow AE \ || \ CD and ED is a transversal.
\angle AEF = \angle CDF [alternate interior angles] - - - - - (III)
In \Delta AEF and \Delta CDF:
\angle AFE = \angle CFD [vertically opposite angles]
\angle AEF = \angle CDF [(from (III)]
AF = FC [from (II)]
Therefore, \Delta AEF \cong \Delta CDF [by AAS congruence rule].
\Rightarrow AE = CD [by CPCT] - - - - - (IV)
From equations (I) and (IV), we can say that:
BE = CD
In quadrilateral EBCD:
BE \ || \ CD and BE = CD
One pair of opposite side is equal and parallel.
Thus, EBCD is a parallelogram.
So, ED \ || \ BC
\Rightarrow EF \ || \ BC
Hence, proved.
Note: We proved that \Delta AEF \cong \Delta CDF.
EF = FD [by CPCT]
[Since EBCD is a parallelogram, ED = BC].
Thus, we can conclude that the parallel mid-line segment is half of the third side of the triangle.
Important!
The line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
Theorem X
The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.

Given: ABC is a triangle, where E is the mid-point of AB. Also, EF \ || \ BC.
Construction: Draw a line segment through C parallel to AB and extend EF to meet this line at D.
To prove: F is the mid-point of AC. That is, AF = FC
Proof: Since E is the mid-point of AB, AE = EB - - - - (I)
In quadrilateral EBCD:
EF \ || \ BC [since ED \ || \ BC]
EB \ || \ DC [by construction]
Both pairs of opposite sides are parallel.
Thus, EBCD is a parallelogram.
We know that "opposite sides of a parallelogram are equal".
EB = DC - - - - (II)
On comparing equation (I) and (II), we get, AE = DC - - - - (III).
Since AE \ || \ DC with transversal ED by construction.
\angle AEF = \angle CDF [alternate interior angles] - - - - (IV)
In \Delta AEF and \Delta CDF:
\angle AEF = \angle CDF [from (IV)]
\angle AFE = \angle CFD [vertically opposite angles]
AE = DC [from (III)]
Therefore, \Delta AEF \cong \Delta CDF [by AAS congruence criterion].
\Rightarrow AF = CF [by CPCT]
Thus, F is the mid-point of AC.
Hence, proved.
