PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

1. Recalling the types and the properties of a quadrilateral

A four-sided closed two-dimensional shape is called a quadrilateral. It has four vertices, four sides and four angles.

Angle sum property of a quadrilateral

The sum of the angles of a quadrilateral is \(360º\).

Proof:

Given: \(ABCD\) is a quadrilateral.

Construction: Join \(BD\).

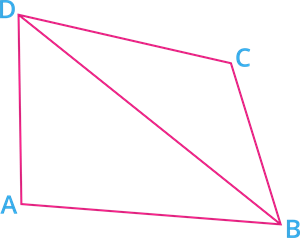
Now, we divided the quadrilateral into two triangles \(BAD\) and \(BCD\).

\(\angle B = \angle ABD + \angle DBC\) - - - - - (I)

\(\angle D = \angle ADB + \angle BDC\) - - - - - (II)

We know that "sum of all the angles of a triangle is \(180^\circ\)".

In \(\Delta BAD\):

\(\angle DAB + \angle ABD + \angle BDA = 180^\circ\) - - - - (III)

Similarly, in \(\Delta BCD\),

\(\angle DBC + \angle BCD + \angle CDB = 180^\circ\) - - - - (IV)

Adding equations (III) and (IV), we get:

\(\angle DAB + \angle ABD + \angle BDA + \angle DBC + \angle BCD + \angle CDB = 180^\circ + 180^\circ\)

Rearrange the angles.

\(\angle DAB + (\angle ABD + \angle DBC) + \angle BCD + (\angle BDA + \angle CDB) = 360^\circ\)

\(\angle A + \angle B + \angle C + \angle D = 360^\circ\) [using equations (I) and (II)]

That is, the sum of the angles of a quadrilateral is \(360^\circ\).

Types of quadrilateral

Name	Picture	Properties
Parallelogram		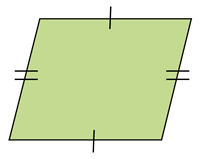1. Opposite sides are equal and parallel. 2. Opposite angles are equal. 3. Diagonals bisect each other.
Square		1. All sides are equal and parallel. 2. All interior angles are \(90^\circ\). 3. Diagonals bisect each other at right angles.
Rectangle		1. Opposite sides are equal and parallel. 2. All interior angles are \(90^\circ\). 3. Diagonals bisect each other.
Rhombus		1. All sides are equal. 2. Opposite angles are equal. 3. Diagonals are perpendicular.
Trapezium		1. The bases of a trapezium are parallel. 2. Sum of adjacent angles on non-parallel sides are supplementary.
Kite		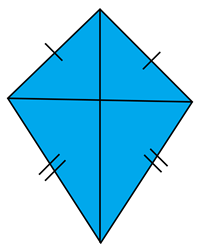1. Diagonals are perpendicular. 2. Diagonals bisect the vertex angles. 3. Non-vertex angles are congruent. 4. Two disjoint pairs of consecutive sides are congruent.