Volume of sphere — lesson. Mathematics CBSE, Class 9.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Sphere:

A sphere is a three-dimensional figure obtained by the revolution of a semicircle about its diameter as an axis.

Volume of a sphere:

Let \(r\) be the radius of a sphere.

Volume of a sphere \(=\)

\frac{4}{3} π r^{3}

cu. units

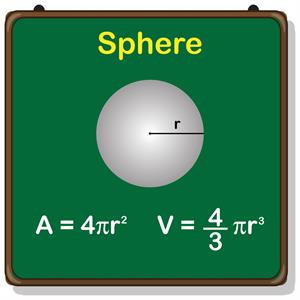
Example:

Find the mass of \(5\) spherical balls, each of diameter \(8.4\) \(cm\).

Solution:

Diameter of the spherical ball \((d)\) \(=\) \(8.4 \ cm\)

Radius of the spherical ball \((r)\) \(=\)

\frac{d}{2} = \frac{8.4}{2} = 4.2

\(cm\)

Volume of the spherical ball \(=\)

\frac{4}{3} π r^{3}

cu. units

\(=\)

\frac{4}{3} \times \frac{22}{7} \times {(4.2)}^{3}

\(=\)

\frac{4}{3} \times \frac{22}{7} \times 4.2 \times 4.2 \times 4.2

\(=\) \(310.464\)

Volume of the spherical ball is \(310.464 \ cm^3\).

Volume of \(5\) spherical balls:

\(=\) \(310.464 \times 5\)

\(=\) \(1552.32\)

Therefore, the volume of \(5\) spherical balls is \(1552.32 \ cm^3\).

Important!

The value of \(\pi\) should be taken as

\frac{22}{7}

unless its value is shared in the problem.

Did you find an error?

1. Volume of sphere