Volume of hemisphere — lesson. Mathematics CBSE, Class 9.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

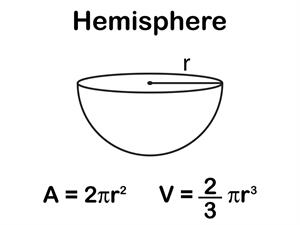
Learn more

Hemisphere:

A one half of a sphere is called a hemisphere.

Volume of a hemisphere:

Let

$r$ be the radius of a sphere.

Volume of a hemisphere

$=$

$\frac{1}{2}$

$\times$ Volume of a sphere

$=$

$\frac{1}{2} \times (\frac{4}{3} π r^{3})$

$=$

$\frac{2}{3} π r^{3}$

Volume of a hemisphere

$=$

$\frac{2}{3} π r^{3}$ cu. units

Example:

The radius of the hemisphere is

$14 \ cm$ . Find the volume of the hemisphere in grams if

$1 \ cm^3 = 0.4 \ g$ .

Solution:

Radius of the hemisphere

$(r)$

$=$

$14 \ cm$

Volume of the hemisphere

$=$

$\frac{2}{3} π r^{3}$ cu. units

$=$

$\frac{2}{3} \times \frac{22}{7} \times 14^{3}$

$=$

$\frac{2}{3} \times \frac{22}{7} \times 14 \times 14 \times 14$

$=$

$5749.33$

$cm^3$

Now, convert

$cm^3$ to

$g$ .

$1 \ cm^3$

$=$

$0.4 \ g$

$5749.33 \ cm^3$

$=$

$5749.33 \times 0.4$

$=$

$2299.732 \ g$

Therefore, the volume of the hemisphere is

$2299.732 \ g$ .

Important!

The value of

$\pi$ should be taken as

$\frac{22}{7}$ unless its value is shared in the problem.

Previous theory

Exit to the topic

Next exercise

Send feedback

Did you find an error?

Send it to us!

2. Volume of hemisphere

Theory: