PDF chapter test TRY NOW
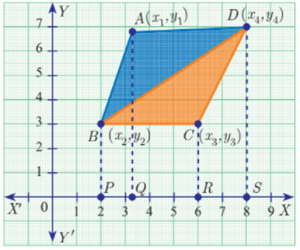
Consider a quadrilateral \(ABCD\) whose vertices are \(A (x_1, y_1)\), \(B (x_2, y_2)\), \(C (x_3, y_3)\) and \(D (x_4, y_4)\) taken in order.
Draw a diagonal \(BD\) and split the quadrilateral into two triangles \(ABD\) and \(BCD\).
 |
Therefore, we have:
Area of the quadrilateral \(ABCD\) \(=\) Area of triangle \(ABD\) \(+\) Area of triangle \(BCD\).
We know that the area of a triangle having its vertices \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\)is
given by:
Area of the triangle \(=\) \(\frac{1}{2}\left[ \left(x_1y_2 + x_2y_3 + x_3y_1\right) - \left(x_2y_1 + x_3y_2 + x_1y_3\right)\right]\) square units.
Therefore, Area of the quadrilateral \(ABCD\) \(=\) \(\frac{1}{2}\left[ \left(x_1y_2 + x_2y_4 + x_4y_1\right) - \left(x_2y_1 + x_4y_2 + x_1y_4\right)\right]\) \(+\) \(\frac{1}{2}\left[ \left(x_2y_3 + x_3y_4 + x_4y_2\right) - \left(x_3y_2 + x_4y_3 + x_2y_4\right)\right]\)
Factor out the common terms and rearrange the terms.
Thus, we have:
Area of the quadrilateral \(ABCD\) \(=\) \(\frac{1}{2}\left[\left(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1\right) - \left(x_2y_1 + x_3y_2 + x_4y_3 + x_1y_4\right)\right]\)
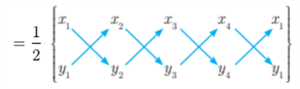
The formula can be easily remembered using the following pictorial representation.
 |
Another form of the formula:
Area of the quadrilateral \(ABCD\) \(=\) \(\frac{1}{2}\left[\left(x_1 - x_3\right)\left(y_2 - y_4\right) - \left(x_2 - x_4\right)\left(y_1 - y_3\right)\right]\) square units.
Example:
Find the area of the quadrilateral joining the vertices \((- 3, 4)\), \((- 5, - 6)\), \((4, - 1)\) and \((1, 2)\).
Solution:
By the formula, we have:
Area of the quadrilateral \(=\) \(\frac{1}{2}\left[\left(x_1 - x_3\right)\left(y_2 - y_4\right) - \left(x_2 - x_4\right)\left(y_1 - y_3\right)\right]\) square units
Substitute the required values in the above formula.
Area of the quadrilateral \(=\) \(\frac{1}{2}\left[\left(-3 - 4\right)\left(-6 - 2\right) - \left(-5 - 1\right)\left(4 - (-1)\right)\right]\)
\(=\) \(\frac{1}{2}\left[(-7)(- 8) - (-6)(4)\right]\)
\(=\) \(\frac{1}{2}\left[56 + 24\right]\)
\(=\) \(\frac{80}{2}\)
\(=\) \(40\)
Therefore, area of the quadrilateral joining the vertices \((- 3, 4)\), \((- 5, - 6)\), \(4, - 1)\) and \((1, 2)\) is \(40\) square units
Register for free to see more content