PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet \(l_1\) and \(l_2\) be two non-vertical lines.
The slope of line \(l_1\) is \(m_1\), and line \(l_2\) is \(m_2\).
Let the inclination of \(l_1\) be \(\theta_1\) and \(l_2\) be \(\theta_2\).
Assume \(l_1\) and \(l_2\) are parallel lines.
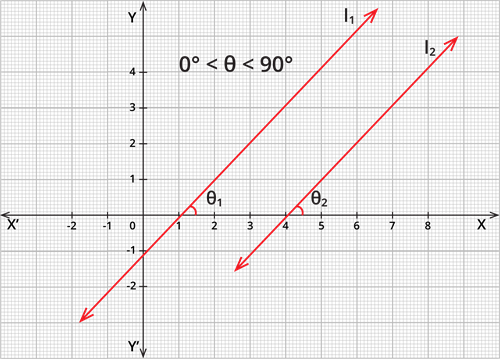
If two lines are parallel, then their corresponding angles are equal.
\(\Rightarrow \theta_1 = \theta_2\)
\(\Rightarrow \tan \theta_1 = \tan \theta_2\)
\(\Rightarrow m_1 = m_2\)
The slopes are equal.
Conversely:
Assume slopes of two lines \(l_1\) and \(l_2\), are equal.
\(\Rightarrow m_1 = m_2\)
\(\Rightarrow \tan \theta_1 = \tan \theta_2\)
\(\Rightarrow \theta_1 = \theta_2\)
\(\Rightarrow\) Corresponding angles are equal.
\(\Rightarrow\) \(l_1\) and \(l_2\) are parallel.
Thus, the non-vertical lines are parallel if and only if their slopes are equal.
If two lines are parallel, then their slopes are equal. That is, \(m_1 = m_2\).
Example:
If a line \(p\) passing through the points \((1, 8)\) and \((2, 13)\) and a line \(q\) passing through the points \((0, -1)\) and \((1, 4)\) are parallel?
Solution:
Let the points passing through the line \(p\) be \(A\) \(=\) \((1, 8)\) and \(B = (2, 13)\).
And, the points passing through the line \(q\) be \(C = (0, -1)\) and \(D = (1, 4)\).
Two lines are parallel if their slopes are equal.
Let us find the slopes of \(p\) and \(q\).
Slope \(=\)
Slope of \(p\) \(=\)
Slope of \(q\) \(=\)
Hence, the slope of \(p\) \(=\) slope of \(q\).
Therefore, the lines \(p\) and \(q\) are parallel.
Important!
The quadrilateral is a parallelogram if the slopes of both pairs of opposite sides are equal.
Register for free to see more content