UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us find the equation of the straight line passing through the point \(A(x_1,y_1)\) and having slope \(m\).
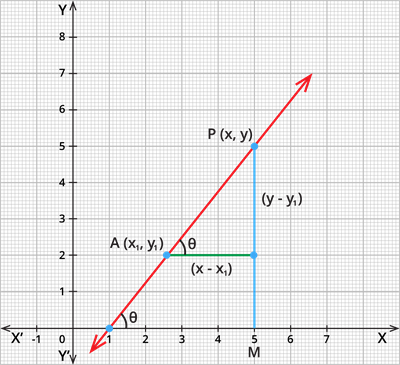
Let \(P(x,y)\) be another point other than \(A\). Then, the slope of the line joining the points \(A\) and \(P\) is given by:
\(m = tan \theta = \frac{y - y_1}{x - x_1}\)
\((x - x_1)m = y - y_1\)
Therefore, the equation of the straight line is \((x - x_1)m = y - y_1\) [Point slope form]
Example:
Find the equation of the line passing through the points \((2,-3)\), and the slope is \(\frac{1}{5}\).
Solution:
Given that \((x_1,y_1) = (2,-3)\) and \(m = \frac{1}{5}\)
Substituting the known values in the formula, \((x - x_1)m = y - y_1\), we get:
\((x - 2)\frac{1}{5} = y + 3\)
\(x - 2 = 5(y + 3)\)
\(x - 2 = 5y + 15\)
\(x - 5y - 15 - 2 = 0\)
\(x - 5y - 17 = 0\)
Therefore, the equation of the straight line is \(x - 5y - 17 = 0\)
Register for free to see more content