PDF chapter test TRY NOW
Cevian:
A cevian is a line segment that extends from one vertex of a triangle to the opposite side.
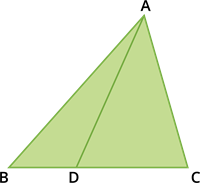 |
In the figure, AD is a cevian from A.
Special Cevians of a Triangle:
- A median is a cevian that divides the opposite side into two equal lengths.
- An altitude is a cevian that is perpendicular to the opposite side.
- An angle bisector is a cevian that bisects the corresponding angle.
Ceva’s Theorem (without proof):
Let ABC be a triangle and let D, E, F be points on lines BC, CA and AB respectively.
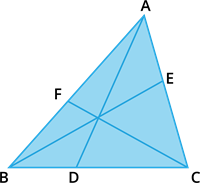 |
Then the cevians AD, BE, CF are concurrent if and only if \frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB} = 1 where the lengths are directed. This also works for the reciprocal of each of the ratios as the reciprocal of 1 is 1.
Example:
The cevians AD, BE and CF of the triangle ABC are congruent. If \frac{BD}{DC} = \frac{2}{5}, \frac{CE}{EA} = \frac{3}{4} and \frac{AF}{FB} = \frac{x}{6}, find the value of x.
Solution:
By Ceva's theorem, we have \frac{BD}{DC} \times \frac{CE}{EA} \times \frac{AF}{FB} = 1.
Substitute the required values in the above equation.
\Rightarrow \frac{2}{5} \times \frac{3}{4} \times \frac{x}{6} = 1
\Rightarrow x = 1 \times \frac{5}{2} \times \frac{4}{3} \times 6
\Rightarrow x = 20
Menelaus Theorem (without proof):
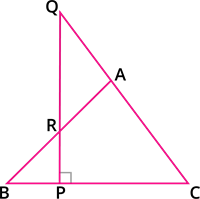 |
A necessary and sufficient condition for points P, Q, R on the respective sides BC, CA, AB (or their extension) of a triangle ABC to be collinear is that \frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = -1 where all segments in the formula are directed segments.
Important!
- Menelaus theorem is also given by BP \times CQ \times AR = − PC \times QA \times RB.
- If any one of the six directed line segments BP, PC, CQ, QA, AR, or RB is interchanged, then the product will be 1.
Example:
On a random board, three pins P, Q, R are punched in the way, BP = 3 cm, CQ = 4 cm, RA = 5 cm, PC = 2 cm, QA = 5 cm, RB = 6 cm, where A, B and C are points such that P lies on BC, Q lies on AC and R lies on AB. Check whether the pins P, Q and R lie on the same straight line.
Solution:
Note that the directed segment AR is interchanged as RA.
By Menelaus theorem, the pins P, Q and R will lie on the same straight line if BP
\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = 1.
\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB} = 1.
Consider the left-hand side of the equation.
\frac{BP}{PC} \times \frac{CQ}{QA} \times \frac{AR}{RB}
Substitute the required values in the above equation.
= \frac{3}{2} \times \frac{4}{5} \times \frac{5}{6}
= \frac{60}{60}
= 1
Therefore, the pins P, Q and R lie on the same straight line.
