Results 1 and 2 on circles and tangents — lesson. Mathematics State Board, Class 10.

UPSKILL MATH PLUS

Learn Mathematics through our AI based learning portal with the support of our Academic Experts!

Learn more

Result $1$ :

A tangent at any point on a circle and the radius through the point are perpendicular to each other.

Explanation:

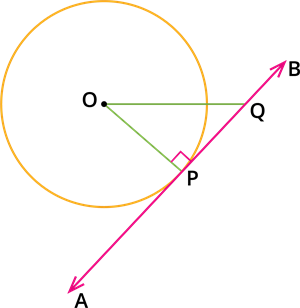The tangent at the point

$P$ on a circle and the radius through the point

$P$ are perpendicular.

That is, the radius

$OP$ makes an angle

$90^{\circ}$ with the tangent

$AB$ at the point

$P$ .

Example:

In the above given figure if

$OP$

$=$

$3$

$cm$ and

$PQ$

$=$

$4$

$cm$ , find the length of

$OQ$ .

Solution:

By the result,

$\angle OPQ$

$=$

$90^{\circ}$ .

So,

$OPQ$ is a right-angled triangle.

By the Pythagoras theorem, we have:

In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

$OQ^2$

$=$

$OP^2$

$+$

$PQ^2$

$OQ^2$

$=$

$3^2$

$+$

$4^2$

$OQ^2$

$=$

$9 + 16$

$OQ^2$

$=$

$25$

$\Rightarrow$

$OQ$

$=$

$\sqrt{25}$

$OQ$

$=$

$5$

Therefore, the measure of

$OQ$

$=$

$5$

$cm$

Result $2$ :

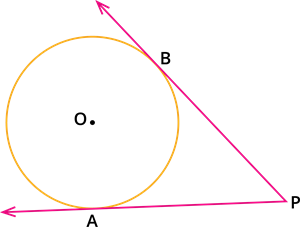
No tangent can be drawn from an interior point of the circle.

Only one tangent can be drawn at any point on a circle.

Two tangents can be drawn from any exterior point of a circle.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

3. Results 1 and 2 on circles and tangents

Theory: