PDF chapter test TRY NOW
Result \(3\):
The lengths of the two tangents drawn from an exterior point to a circle are equal.
Explanation:
 |
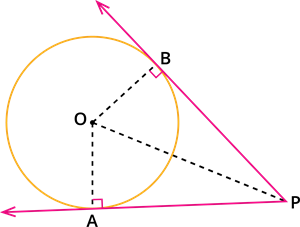The lengths of the two tangents \(PA\) and \(PB\) drawn from an exterior point \(P\) to a circle are equal.
\(\Rightarrow\) \(PA = PB\).
Proof of the result:
By the result \(1\), we have:
A tangent at any point on a circle and the radius through the point are perpendicular to each other.
\(OB\) \(\perp\) \(PB\) and \(OA\) \(\perp\) \(PA\).
Here, \(OA\) and \(OB\) are radius. Hence, they are equal.
The side \(OP\) is a common side to the triangles \(AOP\) and \(BOP\).
Thus, the triangles \(AOP\) and \(BOP\) are congruent.
Therefore, \(PA = PB\).
Example:
In the above given figure if \(OB\) \(=\) \(3\) \(cm\) and \(OP\) \(=\) \(5\) \(cm\), find the length of \(PA\).
Solution:
By the result \(1\), we have:
A tangent at any point on a circle and the radius through the point are perpendicular to each other.
\(\angle OPB\) \(=\) \(90^{\circ}\).
So, \(OPB\) is a right-angled triangle.
By the Pythagoras theorem, we have:
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
\(OP^2\) \(=\) \(OB^2\) \(+\) \(PB^2\)
\(PB^2\) \(=\) \(OP^2\) \(-\)\(OB^2\)
\(PB^2\) \(=\) \(5^2\) \(-\) \(3^2\)
\(PB^2\) \(=\) \(25 - 9\)
\(PB^2\) \(=\) \(16\)
\(\Rightarrow\) \(PB\) \(=\) \(\sqrt{16}\)
\(PB\) \(=\) \(4\)
Thus, the measure of \(PB\) \(=\) \(4\) \(cm\)
By the result \(3\), we have:
The lengths of the two tangents drawn from an exterior point to a circle are equal.
Hence, \(PA\) \(=\) \(PB\).
Therefore, the measure of \(PA\) \(=\) \(4\) \(cm\)
Register for free to see more content