UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreAngle Bisector theorem
Statement: The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the corresponding sides containing the angle.
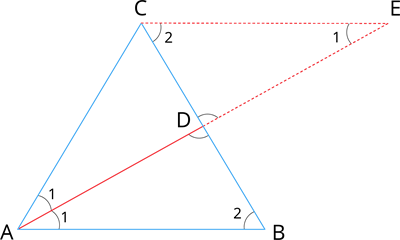
Given: In \(\triangle ABC\), \(AD\) is the internal bisector.
To prove: \(\frac{AB}{AC} = \frac{BD}{CD}\)
Construction: Draw a line through \(C\) parallel to \(AB\). Extend \(AD\) to meet line \(C\) at \(E\).
Proof: Here, \(CE\) and \(AB\) are two parallel lines cut by a transversal line \(BE\).
Then, \(\angle AEC = \angle BAE = \angle 1\) [Alternate angles are equal]
Since \(AD\) is the angle bisector, then \(\angle BAD = \angle DAC\)
In \(\triangle ACE\), \(\angle CAE = \angle CEA\)
Therefore, \(\triangle ACE\) is isosceles.
Thus, \(AC = CE\) ---- (\(1\))
By AA similarity, we have:
\(\triangle ABD \sim \triangle ECD\)
\(\frac{AB}{CE} = \frac{BD}{CD}\)
\(\frac{AB}{AC} = \frac{BD}{CD}\) [Using equation (\(1\))]
Hence, we proved.
The converse of the angle bisector theorem
Statement: If a straight line through one vertex of a triangle divides the opposite side internally in the ratio of the other two sides, then the line bisects the angle internally at the vertex.
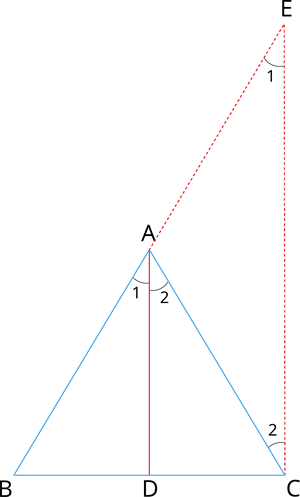
Given: \(ABC\) is a triangle. \(AD\) divides \(BC\) in the ratio of the sides containing the angles \(\angle A\) to meet \(BC\) at \(D\).
That is, \(\frac{AB}{AC} = \frac{BD}{DC}\) ---- (\(1\))
To prove: \(AD\) bisects \(\angle A\). That is, \(\angle 1 = \angle 2\)
Construction: Draw \(CE \parallel DA\). Extend \(BA\) to meet at \(E\).
Proof: Let us assume \(\angle BAD = \angle 1\) and \(\angle DAC = \angle 2\).
Since \(DA \parallel CE\) and \(AC\) is the transversal, then, we have:
\(\angle BAD = \angle AEC = \angle 1\) [Corresponding angles are equal]
\(\angle DAC = \angle ACE = \angle 2\) [Alternate angles are equal]
Consider \(\triangle BCE\). By Thales theorem, we have:
\(\frac{BA}{AE} = \frac{BD}{DC}\) ---- (\(2\))
From equations (\(1\)) and (\(2\)), we have:
\(\frac{AB}{AC} = \frac{BA}{AE}\)
\(AC = AE\) [Cancelling \(AB\)] ---- (\(3\))
Therefore, \(\triangle ACE\) is isosceles by equation (\(3\)).
\(\Rightarrow \angle 1 = \angle 2\)
Since \(\angle BAD = \angle 1\) and \(\angle DAC = \angle 2\), then \(AD\) bisects \(\angle A\).
Hence, we proved.
Register for free to see more content