PDF chapter test TRY NOW
Basic proportionality theorem or Thales theorem
Theorem 1: A straight line is drawn parallel to one side of a triangle intersecting the other two sides divides the sides in the same ratio.
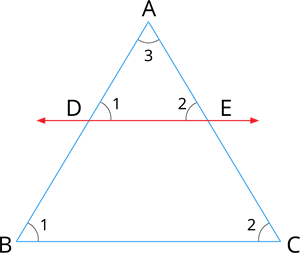
Given: In a triangle, \(ABC\), \(D\) is a point on \(AB\) and \(E\) is a point on \(AC\).
To prove: \(\frac{AD}{DB} = \frac{AE}{EC}\)
Construction: Draw a line \(DE \parallel BC\).
Proof: Here, \(\angle ABC = \angle ADE = \angle 1\) [Corresponding angles are equal because \(DE \parallel BC\)]
\(\angle ACB = \angle AED = \angle 2\) [Corresponding angles are equal because \(DE \parallel BC\)]
\(\angle BAC = \angle DAE = \angle 3\) [Both triangles have a common angle]
\(\triangle ABC \sim \triangle ADE\) [By AAA similarity]
\(\frac{AB}{AD} = \frac{AC}{AE}\) [Corresponding sides are proportional]
\(\frac{AD + DB}{AD} = \frac{AE + EC}{AE}\)
\(1 + \frac{DB}{AD} = 1 + \frac{EC}{AE}\)
\(\frac{DB}{AD} = \frac{EC}{AE}\)
\(\frac{AD}{DB} = \frac{AE}{EC}\) [Taking reciprocal]
Hence, we proved.
Corollary:
In a \(\triangle ABC\), a straight line \(DE\) intersects \(AB\) at \(D\) and \(AC\) at \(E\) and is parallel to \(BC\), then prove that
(i) \(\frac{AB}{AD} = \frac{AC}{AE}\) (ii) \(\frac{AB}{DB} = \frac{AC}{EC}\)
Proof:

(i) By Thales theorem, we have:
\(\frac{AD}{DB} = \frac{AE}{EC}\)
\(\frac{DB}{AD} = \frac{EC}{AE}\)
Adding \(1\) on both sides of the equation, we have:
\(\frac{DB}{AD} + 1 = \frac{EC}{AE} + 1\)
\(\frac{DB + AD}{AD} = \frac{EC + AE}{AE}\)
\(\frac{AB}{AD} = \frac{AC}{AE}\)
Hence, we proved.
(ii) By Thales theorem, we have:
\(\frac{AD}{DB} = \frac{AE}{EC}\)
Adding \(1\) to both sides of the equation, we have:
\(\frac{AD}{DB} + 1 = \frac{AE}{EC} + 1\)
\(\frac{AD + DB}{DB} = \frac{AE + EC}{EC}\)
\(\frac{AB}{DB} = \frac{AC}{EC}\)
Hence, we proved.
Converse of Basic proportionality theorem or Converse of Thales theorem.
Theorem 2: If a straight line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
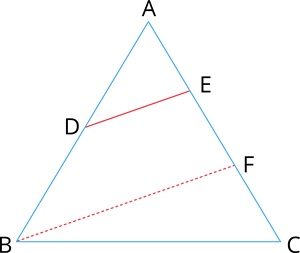
Given: In \(\triangle ABC\), \(\frac{AD}{DB} = \frac{AE}{EC}\)
To prove: \(DE \parallel BC\)
Construction: If \(DE\) is not parallel to \(BC\), then draw \(BF \parallel DE\).
Proof: Since \(DE \parallel BC\), and two sides \(AB\) and \(AC\) are divided in the same ratio, then by Thales theorem, we get:
\(\frac{AD}{DB} = \frac{AE}{EC}\) ---- (\(1\))
\(\frac{AD}{DB} = \frac{AF}{FC}\) ---- (\(2\))
From equations (\(1\)) and (\(2\)), we get:
\(\frac{AE}{EC} = \frac{AF}{FC}\)
Adding \(1\) to both sides, we get:
\(\frac{AE}{EC} + 1 = \frac{AF}{FC} + 1\)
\(\frac{AE + EC}{EC} = \frac{AF + FC}{FC}\)
\(\frac{AC}{EC} = \frac{AC}{FC}\)
\(EC = FC\) [Cancelling \(AC\)]
This is true only if \(F\) and \(E\) coincide.
Therefore, \(DE \parallel BC\)
Hence, we proved.
