PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoTwo integers, \(a\) and \(b\), are said to be congruent modulo \(n\) if and only if their difference is divisible by \(n\). It can be written as
\(a \equiv b (mod \ n)\)
In other words, the two integers, \(a\) and \(b\), is the difference of the integer multiple of congruence modulo \(n\). That is, \(b - a = kn\) for some integer \(k\).
Here, \(n\) is called the modulus of the congruence.
Example:
\(39 \equiv 4 (mod \ 5)\). Here, \(5\) is the modulus of the congruence because \(39 - 4 = 35\) is divisible by \(5\).
Consider the following examples on how to find the congruence modulo.
Example:
1. Find \(3 (mod \ 2)\)
Solution:
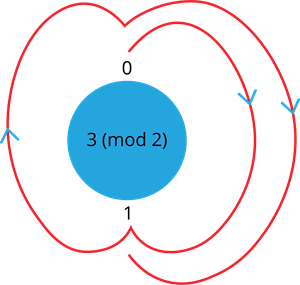
Consider the possible remainders for the number with mod \(2\) are \(0\), \(1\).
To find the remainder of the given number, start at \(0\) and go through \(3\) numbers in a clockwise direction. The \(3\) numbers would go in a cycle starting from \(0\). They are \(1\), \(0\), \(1\). Since the cycle ends at the remainder of \(1\), the answer for \(3 (mod \ 2)\) is \(1\).
Therefore, \(3 \equiv 1 (mod \ 2)\)
2. Find \(-3 (mod \ 2)\)
Solution:
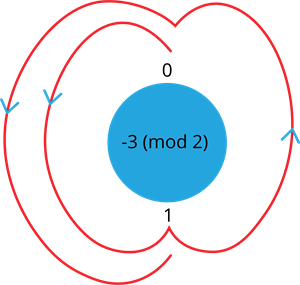
Consider the possible remainders for the number with mod \(2\) are \(0\), \(1\).
To find the remainder of the given number, start at \(0\) and go through \(3\) numbers in a anticlockwise direction(because the number has a negative sign). The \(3\) numbers would go in a cycle starting from \(0\). They are \(1\), \(0\), \(1\). Since the cycle ends at the remainder of \(1\), the answer for \(-3 (mod \ 2)\) is \(1\).
Therefore, \(-3 \equiv 1 (mod \ 2)\)
Register for free to see more content