4. Problems involving angle of elevation and depression

Kumar takes walks every evening. One evening, he observes a bird flying with an angle of elevation of $60^{\circ}$. He also observes a dog right beneath the bird with an angle of depression of $30^{\circ}$. If the height of Kumar is $1.5 \ m$, then find the altitude of the bird from the dog.

 

Solution:

 

 

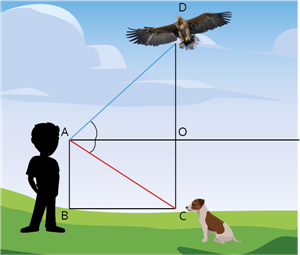
Let $AB$ denote the height of Kumar. Then, $AB = 1.5 \ m$.

 

$CD$ is the altitude of the bird from the ground. Through $A$, draw $AO \perp CD$.

 

The angle of elevation is $\angle OAD = 60^{\circ}$.

 

The angle of depression is $\angle OAC = 30^{\circ}$.

 

Let $h$ denote the altitude of the bird from the ground.

 

That is, $CD = h$.

 

Then, $OD = CD - OC = h - 1.5$

 

In right triangle $OAC$, $tan \ \theta = \frac{OC}{AO}$

 

$tan \ 30^{\circ} = \frac{1.5}{AO}$

 

$\frac{1}{\sqrt{3}} = \frac{1.5}{AO}$

 

$AO = 1.5\sqrt{3}$ ---- ($1$)

 

In right triangle $OAD$, $tan \ \theta = \frac{OD}{AO}$

 

$tan \ 60^{\circ} = \frac{h - 1.5}{1.5\sqrt{3}}$ [Using equation ($1$)]

 

$\sqrt{3} = \frac{h - 1.5}{1.5\sqrt{3}}$

 

$1.5\sqrt{3}(\sqrt{3}) = h - 1.5$

 

$1.5 \times 3 = h - 1.5$

 

$4.5 = h - 1.5$

 

$4.5 + 1.5 = h$

 

$6 = h$

 

Therefore, the altitude of the bird from the dog is $6 \ m$.