PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet \(ABC\) be a right angled triangle.
Let \(0^\circ < \theta < 90^\circ\).
\(\sin \theta = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{AB}{AC}\)
\(\cos \theta = \frac{\text{Adjacent side}}{\text{Hypotenuse}} = \frac{BC}{AC}\)
\(\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{BC}\)
\(\text{cosec}\: \theta = \frac{\text{Hypotenuse}}{\text{Opposite side}} = \frac{AC}{AB}\)
\(\sec \theta = \frac{\text{Hypotenuse}}{\text{Adjacent side}} = \frac{AC}{BC}\)
\(\cot \theta = \frac{\text{Adjacent side}}{\text{Opposite side}} = \frac{BC}{AB}\)
\(\tan \theta = \frac{\sin \theta}{\cos \theta}\)
\(\cot \theta = \frac{\cos \theta}{\sin \theta} = \frac{1}{\tan \theta}\)
\(\text{cosec}\: \theta = \frac{1}{\sin \theta}\)
\(\sec \theta = \frac{1}{\cos \theta}\)
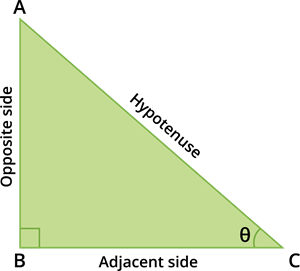
Trigonometric ratio table
Register for free to see more content