PDF chapter test TRY NOW
| \(\sin (90^\circ - \theta) = \cos \theta\) | \(\cos (90^\circ - \theta) = \sin\theta\) |
| \(\tan (90^\circ - \theta) = \cot \theta\) | \(\cot (90^\circ - \theta) = \tan \theta\) |
| \(\text{cosec} (90^\circ - \theta) = \sec \theta\) | \(\sec (90^\circ - \theta) = \text{cosec}\: \theta\) |
Visual proof of Trigonometric complementary angle
Let us consider a semicircle of radius \(1\) unit.
Assume \(\angle BOA = \theta\) and radius \(= OB = 1\).
\(\Rightarrow \angle BOC = 90^\circ - \theta\).
\(\Rightarrow OABC\) forms a rectangle.
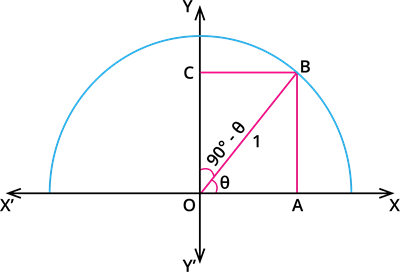
Consider a triangle \(OAB\):
\(\cos \theta = \frac{\text{Adjacent side to}\ \theta}{\text{Hypotenuse}}\)
\(\cos \theta = \frac{OA}{OB}\)
\(\cos \theta = \frac{OA}{1}\)
\(\cos \theta = OA\) - - - - - (I)
Similarly, \(\sin \theta = \frac{\text{Opposite side to}\ \theta}{\text{Hypotenuse}}\)
\(\sin \theta = \frac{AB}{OB}\)
\(\sin \theta = \frac{AB}{1}\)
\(\sin \theta = AB\) - - - - - (II)
Consider a triangle \(BOC\):
\(\cos (90^\circ - \theta) = \frac{\text{Adjacent side to}\ (90^\circ - \theta)}{\text{Hypotenuse}}\)
\(\cos (90^\circ - \theta) = \frac{OC}{OB}\)
\(\cos (90^\circ - \theta) = \frac{OC}{1}\)
\(\cos (90^\circ - \theta) = OC\) - - - - - (III)
Similarly, \(\sin (90^\circ - \theta) = \frac{\text{Opposite side to}\ (90^\circ - \theta)}{\text{Hypotenuse}}\)
\(\sin (90^\circ - \theta) = \frac{BC}{OB}\)
\(\sin (90^\circ - \theta) = \frac{BC}{1}\)
\(\sin (90^\circ - \theta) = BC\) - - - - - (IV)
Since \(OABC\) is a rectangle, opposite sides are equal.
\(OA = BC\) and \(AB = OC\)
\(\cos \theta = \sin (90^\circ - \theta)\) and \(\sin \theta = \cos (90^\circ - \theta)\).
Hence, we proved.
Important!
\((\sin \theta)^2 = \sin^2 \theta\)
\((\cos \theta)^2 = \cos^2 \theta\)
\((\tan \theta)^2 = \tan^2 \theta\)
\((\text{cosec}\: \theta)^2 = \text{cosec}^2\: \theta\)
\((\sec \theta)^2 = \sec^2 \theta\)
\((\cot \theta)^2 = \cot^2 \theta\)
Register for free to see more content